https://www.youtube.com/watch?v=SzJ46YA_RaA ーーーーー この動画の内容を要約し、それぞれについて詳しく解説してください。
動画内容の要約と詳細解説
1. 基礎理論 (Fundamental Theory of Computer Science)
コンピューターサイエンスの**「何を計算できるか」「どのように効率よく計算するか」**という根本的な問いを扱う分野です。1-1. チューリングマシンと計算可能性理論
- チューリングマシン: 理論コンピューターサイエンスの父であるアラン・チューリングによって形式化された、汎用コンピューターのシンプルな概念モデルです([00:00:49])。
- 現代のコンピューターのRAMにあたる無限に長いテープ、CPUにあたるヘッド、そして命令リストから構成されます([00:01:09])。
- 計算可能性理論 (Computability Theory): コンピューターで何が解けて、何が解けないのかを分類しようとする分野です([00:01:46])。
- 有名な例として、**「停止問題 (Halting Problem)」**があります。これは、あるプログラムが永遠に実行を続けるのか、それとも停止するのかを予測しようとする問題で、その性質上、コンピューターで解くことが不可能な問題として知られています([00:01:54])。
1-2. 計算量理論 (Computational Complexity)
- 理論的には解ける問題でも、実際にはメモリを使いすぎたり、宇宙の寿命よりも長いステップ数を要したりして、実用上解けない問題があります([00:02:04])。
- この分野は、問題の規模が大きくなったときに、解決にかかる時間やリソースがどれくらい増えるか(スケーリング)によって問題を分類します([00:02:11])。
1-3. アルゴリズムと情報理論
- アルゴリズム: ハードウェアやプログラミング言語に依存しない、特定の問題を解くための手順のセット(いわば「レシピ」)です([00:02:36])。
- 同じ最終結果(例: 数値をソートする)を得るにしても、アルゴリズムによって効率が大きく異なるため、その効率性をアルゴリズム複雑性として研究します([00:02:54])。
- 情報理論: 情報の特性(測定、保存、通信)や、データ圧縮の仕組みなどを研究する分野です([00:03:04])。
- 符号理論と暗号理論 (Coding Theory & Cryptography): 暗号化によってインターネット上で送信される情報を秘密に保つために非常に重要で、複雑な数学的問題に頼って情報をロックします([00:03:21])。
2. コンピューター工学 (Computer Engineering)
コンピューターのハードウェア設計から、それを動かすためのソフトウェアの基礎までを扱う分野です。2-1. コンピューターアーキテクチャとCPU
- CPU (中央処理装置): コンピューターの中核であり、実行されるすべてのタスクがここを通ります([00:04:07])。
- スケジューラーというプログラムが、複数のタスクを切り替え、最も効率的な方法で処理を進めるように制御します([00:04:14])。
- マルチプロセッシングによって複数のコアで並列処理が可能になりますが、スケジューラーの仕事はさらに複雑になります([00:04:25])。
- 異なるアーキテクチャ:
- CPU: 汎用的なタスクに適しています([00:04:43])。
- GPU (グラフィックス処理ユニット): グラフィックス処理に最適化されています([00:04:44])。
- FPGA: 特定の狭い範囲のタスクを超高速で実行できるようにプログラム可能です([00:04:47])。
2-2. ソフトウェアの階層
- プログラミング言語: 人間がコンピューターに何をすべきかを伝える方法です([00:04:56])。
- アセンブリ言語のようなハードウェアに近い低水準言語から、PythonやJavaScriptのようなウェブサイトやアプリ用の高水準言語まで様々です([00:05:05])。
- コンパイラ: プログラマーが書いたコードを、CPUが理解できる生の命令に変換するプログラムです([00:05:19])。
- オペレーティングシステム (OS): コンピューター上で最も重要なソフトウェアであり、私たちが直接操作し、他のすべてのプログラムがハードウェア上でどのように実行されるかを制御します([00:05:38])。
2-3. ソフトウェアエンジニアリング
- コンピューターに何をすべきかを指示する命令の束を書く分野です。
- クリエイティブなアイデアを論理的な命令に変換し、実行効率を最大限に高め、エラーを可能な限りなくす技術や設計哲学が研究されます([00:05:58])。
- その他の重要分野: 複数のコンピューターを連携させるネットワーキング、大量データの保存と検索、システム性能の評価、リアルなグラフィックスの作成などが含まれます([00:06:18])。
3. 応用 (Applications)
コンピューターを現実世界の問題解決に活用するための分野です。3-1. 人工知能 (AI) と機械学習 (ML)
- 人工知能 (AI): コンピューターシステムが自ら考えることができるように開発する、コンピューターサイエンス研究の最先端です([00:07:18])。
- 機械学習 (ML): AI研究で最も目立つ分野で、大量のデータからコンピューターが学習するためのアルゴリズムと技術を開発し、その学習結果を意思決定や分類などの有用なタスクに活用します([00:07:29])。
3-2. データと認識
- コンピュータービジョン: 人間のようにコンピューターが画像内の物体を「見る」ことができるようにすることを目指します([00:07:44])。
- 自然言語処理 (NLP): コンピューターが人間の言語を理解し、コミュニケーションしたり、言葉の形で存在する大量のデータを分析したりすることを目指します([00:07:56])。
- ビッグデータとIoT:
- ビッグデータ: 大量のデータを管理・分析し、そこから価値を引き出す方法を探求します([00:08:16])。
- IoT (モノのインターネット): 日常の物体にデータ収集と通信の機能を加え、さらに多くのデータを生み出す分野です([00:08:22])。
3-3. その他の応用分野
- 最適化問題: 最良の経路や最も効率的な組み合わせを見つける問題(例: 旅行で費用対効果が最も高い旅程を見つける)で、ビジネスで大きなコスト削減につながります([00:06:41])。
- ハッキング: コンピューターシステムの弱点を見つけて悪用しようとする分野です([00:08:33])。
- 計算科学 (Computational Science): コンピューターを使い、物理学から神経科学まで、シミュレーションを通じて科学的な問いに答えることを助けます。この際、世界最強のコンピューター(スーパーコンピューティング)が利用されることがあります([00:08:40])。
- ヒューマン・コンピューター・インタラクション (HCI): コンピューターシステムを使いやすく直感的に設計する方法を研究します([00:08:52])。
- VR/AR (仮想現実/拡張現実) やテレイグジスタンス(遠隔臨場感)など、現実の体験を拡張・代替する技術も含まれます([00:09:00])。
- ロボティクス: コンピューターに物理的な実体を与える分野で、ルンバのような掃除ロボットから、人間のようなインテリジェントな機械の実現を目指します([00:09:07])。
「Map of Computer Science(コンピューターサイエンスの地図)」動画内容要約
1. 基礎理論 (Fundamental Theory of Computer Science)
2. コンピューター工学 (Computer Engineering)
3. 応用 (Applications)
「Map of Computer Science(コンピューターサイエンスの地図)」詳細解説
1. 基礎理論 (Fundamental Theory of Computer Science)
1-1. チューリングマシンと計算可能性理論
1-2. 計算量理論 (Computational Complexity)
1-3. アルゴリズムと情報理論
2. コンピューター工学 (Computer Engineering)
2-1. コンピューターアーキテクチャとCPU
2-2. ソフトウェアの階層
2-3. ソフトウェアエンジニアリング
3. 応用 (Applications)
3-1. 人工知能 (AI) と機械学習 (ML)
3-2. データと認識
3-3. その他の応用分野
参考文献
この動画の内容は「少し触ったことがある」人にも分かりやすいよう、ポイントを整理しながら解説します。コンピューターサイエンスの全体像をさらに具体的なトピックや例を交えて紹介します。
基礎理論
計算の「限界や効率」に関する理論です。
-
チューリングマシン 単純な仕組みで、現代のパソコンが何でも計算できる原理を説明します。
-
停止問題 すべてのプログラムが本当に終わるかどうか、パソコンでも絶対に判定できない「限界」があることの代表例です。
-
アルゴリズムと効率 例えば数字の並び替え(ソート)一つでも、やり方次第で何倍も計算の速さが違います。「O(n)」のような式で難しさを表す方法が使われます。
-
情報・暗号理論 画像などのデータを圧縮したり、暗号化して安全に通信したりする仕組みです。
コンピューター工学
PCやスマホの「仕組み」と、動かすための基本ソフト開発です。
-
CPU・GPU・FPGA 普段はCPUがいろいろな処理を計算していますが、画像やゲームはGPU、特化型処理はFPGA…など役割分担があります。
-
プログラミング言語 C言語やPythonなどの違いは、「機械寄りか人間寄りか」「書きやすさ・動かしやすさ」などです。
-
OSやコンパイラ WindowsやMacのようなOS、プログラムを機械語に直すコンパイラがシステムの基盤として働いています。
-
ソフトウェア設計 バグが出にくく効率のいいプログラムの書き方や設計方法を研究します。
応用
コンピューターが現実世界でどう活かされているかです。
-
人工知能・機械学習 たくさんのデータから「学習」し、画像認識や自動運転、SNSのレコメンドなどに使われています。
-
ビッグデータ・IoT スマート家電や各種センサーから集まる大量データを分析して、価値を生み出します。
-
インタラクション・ロボット スマホのタッチ操作、VR体験、掃除ロボットなど、人と機械がより自然に関われる工夫も進められています。
-
最適化・ハッキング・シミュレーションなど 組み合わせの最適化問題や安全面(ハッキング)、科学研究用のシミュレーションまで幅広い応用があります。
これらが動画で語られた「コンピューターサイエンス」の基本的な構造と応用例です。コンピュータを使った実際の体験がある方でも、体系を把握することで、より深く理解できる内容になっています。
すでに日常的にコンピューターサイエンスと関わっている場合、この動画の内容は、分野の全体像や領域間の関係性を俯瞰的に整理し直す上で有用です。それぞれの柱ごとに、実務や日常に直結する観点を踏まえて詳細に解説します。
基礎理論
計算可能性や効率性の理論は、アルゴリズム設計やシステム設計に日々直結しています。
-
チューリングマシン・計算可能性 計算不可能な問題(停止問題等)や、ランダム化アルゴリズム、自己記述性などの理論的側面は、多くの実アプリケーションの限界値を理解する上で基盤となります。
-
計算量理論・複雑度クラス 多数の現実問題はP/NP境界、NPハード、NP完全で議論されることが多いです。最適化や近似・ヒューリスティック設計の選択時にもここが分岐点となります。
-
アルゴリズム、情報理論、暗号 ソートや探索のアルゴリズム効率化、圧縮、誤り訂正、TLS等暗号プロトコルの安全設計まで、実用実装でも理論知識が不可欠です。
コンピューター工学
ハード・ソフトの両面から、効率や拡張性、性能最適化が常に問われます。
-
CPU/GPU/FPGA/アーキテクチャ 並列処理、非同期I/O、メモリ階層設計、アーキテクチャ固有の最適化など、計算資源の最大活用が現場で求められます。
-
言語・コンパイラ・OS 適材適所の言語選択、JIT/Cross-compiler、オペレーティングシステムのリソース管理やスケジューラ調整、デバッグ・テスト工学などが不可欠な知識となります。
-
ソフトウェアエンジニアリングとネットワーク バージョン管理、CI/CD、自動テスト、大規模システム設計、分散システムやサービス指向アーキテクチャとの接続等、実践的な工学手法が密接に絡みます。
応用分野
現実的な利用場面から高度な技術まで幅広くカバーされます。
-
人工知能・機械学習 データ前処理、モデル選択、ハイパーパラメータチューニング、MLops、オンデバイス学習など、AI/ML活用の全行程が含まれます。
-
コンピュータビジョン・自然言語処理(NLP) 画像認識のためのdeep learning、テキスト分類や多言語対応、知識グラフ・セマンティック検索の現場実装が求められます。
-
ビッグデータ・IoT 分散処理プラットフォーム(Spark, Hadoop等)、リアルタイム解析、センシングデータの収集とクラウド連携、ストリームデータ処理技術。
-
最適化・セキュリティ・HCI・ロボティクス 組合せ最適化やヒューリスティクスの実務応用、サイバーセキュリティ設計、ユーザー体験最適化、ロボティクスでのセンシング・制御理論応用まで現場で幅広く使われます。
日々の業務やプロジェクトで「なぜこの技術選択をするのか」「実装上のボトルネックはどこか」という視点で理論と実装を統合しながら考えると、この動画の全体知識がますます活きてくるはずです。
コンピューターサイエンスの全体地図と戦略的フロンティア:基礎理論、工学、応用による現代技術の構造的理解
第I部:導入 — コンピューターサイエンスの三位一体構造
1.1 CS地図の定義:基礎理論、工学、応用の相互作用
コンピューターサイエンス(CS)は、単なるプログラミングやハードウェア設計の集合体ではなく、計算という現象を根源から解明し、それを実現し、社会に適用する構造的な領域として捉えられる。この領域は、計算の「根源的な可能性」(基礎理論)、「効率的な実現」(コンピューター工学)、そして「社会的価値の創出」(応用)という三つの主要な柱によって支えられている。これら三位一体の要素は、現代において相互にフィードバックし合い、ダイナミックに進化する。 かつて、CSの進歩は主にコンピューター工学の発展、特にムーアの法則によるトランジスタ集積度の指数関数的な増加によって推進されてきた。しかし、物理的限界に直面する現代では、応用分野、とりわけ人工知能(AI)や機械学習(ML)からの爆発的な計算需要が、理論的基盤の再評価(例:量子コンピューティングへの対応)を促し、工学に対して特化型アーキテクチャ(例:TPUやチップレット)という具体的な設計指針を与えている。このパラダイムシフトは、CSの進歩が特定の技術的ブレイクスルーだけでなく、三つの柱全体の戦略的な協調によって規定される時代へと移行したことを示唆する。1.2 現代技術における三柱の重要性の高まり
基礎理論が定める計算の限界(P vs NP問題や停止問題)は、工学的な実現の枠組みを規定する。例えば、量子コンピューティングが既存の暗号技術にもたらす理論的な脅威は、工学および応用分野におけるセキュリティインフラの抜本的な再構築(量子耐性暗号への移行)を不可避なものとしている。このように、CSの三つの柱はそれぞれ独立しているのではなく、限界、最適化、そして社会実装という連鎖的な関係を通じて、現代の技術フロンティアを共同で定義している。第II部:基礎理論 — 計算可能性の限界と効率性の追求
基礎理論の柱は、コンピューターサイエンスの根幹をなす「何が可能で、何が不可能か」という数学的基盤を定める。これは現代のアルゴリズム設計、セキュリティ、ソフトウェア検証の根本を規定する。2.1 計算の形式化と限界: チューリングマシンと停止問題
理論コンピューターサイエンスの父であるアラン・チューリングによって形式化されたチューリングマシン(TM)は、現代の汎用コンピューターのシンプルな概念モデルである [動画内容]。これは、現代のRAMにあたる無限に長いテープ、CPUにあたるヘッド、そして命令リストから構成され、あらゆる電子計算機の数学的基盤を提供する [動画内容]。 この形式化に基づいて、計算可能性理論は、コンピューターで解ける問題(計算可能)と解けない問題(計算不能)を厳密に分類する役割を担う [動画内容]。その中でも最も有名な例が「停止問題(Halting Problem)」である。これは、特定のプログラムがある入力に対して永遠に実行を続けるのか、それとも必ず停止するのかを予測しようとする問題であり、その性質上、コンピューターで解くことが不可能な問題として知られている [動画内容]。 この停止問題の決定不可能性は、単なる数学的興味で終わらない。これはソフトウェア工学、特に高信頼性システムにおける形式検証(Formal Verification)の限界を定める。例えば、PVS(Prototype Verification System)のような検証ツールは、プログラムの終了解析を行う際、停止問題がアンデシダブルであるという理論的な制約を前提としなければならない 。そのため、プログラムの完全な自動検証、特にデッドロックや無限ループの発生を一般的に保証することは不可能であり、検証技術は、形式的な意味論的概念の導入や、人間による厳密な定義を加えること、あるいは検証のスコープを制限することを余儀なくされる 。この理論的な限界は、高リスクな航空宇宙、医療、金融システム開発における品質保証(QA)戦略の基礎となり、ソフトウェア検証のコストと複雑性を増大させる主要因となっている。2.2 計算量理論:効率性のヒエラルキーとP vs. NP
基礎理論の次の重要な課題は、理論的には解ける問題であっても、実際にはメモリを使いすぎたり、途方もないステップ数を要したりして、実用上解けない問題を分類することである [動画内容]。この計算量理論の分野は、問題の規模()が大きくなったときに、解決にかかる時間やリソースがどれくらい増えるか(スケーリング)によって問題を分類する [動画内容]。 この分野の中心に位置するのが、「P vs. NP問題」である。これは、多項式時間で解ける問題(Pクラス)と、解の検証が多項式時間で可能な問題(NPクラス)が同一であるかどうかを問う、コンピューターサイエンス最大の未解決課題である 。 P vs. NP問題は、クレイ数学研究所が選定した七つのミレニアム懸賞問題の一つであり、最初の正解者には100万ドルの賞金がかけられている 。この問題の解決は、その帰結が計算理論を超えて、数学、暗号技術、アルゴリズム研究、人工知能、経済学など多岐にわたる分野に根本的な変化をもたらすため、極めて戦略的な重要性を持つ 。特に、P=NPが証明されれば、現在困難とされているNP完全問題(例:巡回セールスマン問題、多くの最適化問題 [動画内容])が効率的に解けるようになり、ロジスティクス、創薬、スケジューリングにおける完全な最適解が瞬時に得られるようになる。この場合、現在のビジネスモデル(複雑性に基づく暗号の安全性の前提など)は一夜にして無価値となり、経済構造そのものが変革される可能性がある。現在の多くの業界はP≠NPを暗黙の前提としており、この前提の下で近似アルゴリズムやヒューリスティクスが開発されている。 計算量クラスの分類と産業的意義| クラス | 定義 | 解決にかかる時間(最悪ケース) | 実用性 | 代表的な問題(例) |
| P (Polynomial) | 多項式時間で解ける | 問題規模 の多項式 | 容易に解ける(効率的) | ソート、最短経路探索 |
| NP (Non-deterministic Polynomial) | 解の検証が多項式時間で可能 | 指数関数的 (P≠NPが証明された場合) | 解の発見は困難 | 充足可能性問題、巡回セールスマン問題 |
| NP-Complete (NP-C) | NPクラスで最も困難な問題群 | 指数関数的 | 非効率的だが、最適化の鍵 | クリック問題、部分集合和問題 |
| Undecidable | アルゴリズムで解が存在しない | 無限(実行が停止しない) | 不可能 | 停止問題 |
2.3 情報と暗号の理論的土台
アルゴリズムは、ハードウェアや言語に依存しない、特定の問題を解くための手順のセットであり、その効率性はアルゴリズム複雑性として研究される [動画内容]。これと並行して、情報理論は、情報の特性(測定、保存、通信)やデータ圧縮の仕組みを研究する [動画内容]。クロード・シャノンは、この分野で情報の測定単位「ビット」を形式的に定義し、情報理論の普遍的な数学的基礎を築いた功績を持つ 。彼の研究は、符号理論と暗号理論の基盤となり、また彼は1956年のダートマス会議の共催者として、初期の人工知能研究にも貢献した 。暗号理論は、複雑な数学的問題を利用して情報をロックし、インターネット上の秘密通信を可能にする [動画内容]。 しかし、現代の暗号技術は、新たな理論的課題、すなわち量子コンピューティングの脅威に直面している。ピーター・ショアが1994年に開発したShorのアルゴリズムは、古典的なコンピューターでは計算不可能なタスクである大規模な整数の素因数分解を、量子コンピューター上で指数関数的に高速に解くことができる 。 公開鍵暗号システム(RSAやECCなど)の安全性は、この素因数分解の困難さに依存しているため、十分な能力を持つ量子コンピューターが出現すれば、これらの暗号化手法は無力化される 。この事態は、グローバルなデータセキュリティインフラにとって壊滅的な脅威となる。特に、2048ビットのRSA鍵であっても、強力な量子コンピューターを用いれば数時間で破られる可能性があると予測されている 。 この理論的脅威に対処するため、世界中の政府や組織は、量子攻撃に耐性のある数学的問題(主に格子ベースの暗号)に基づくポスト量子暗号(PQC)への移行を急いでいる 。NISTはPQCの標準化プロセスを主導しており、すでにCRYSTALS-Dilithium(デジタル署名)やCRYSTALS-KYBER(鍵確立)などの新しいアルゴリズムが標準として選定されている 。量子コンピューターがまだ大規模ではない現状においても、攻撃者が将来の解読を目的として現在の暗号化データを収集する「Harvest Now, Decrypt Later」攻撃を防ぐため、PQCへの移行は待ったなしの産業的な義務となっている。第III部:コンピューター工学 — ハードウェアの特化とソフトウェアの分散
コンピューター工学の柱は、基礎理論の制約内で、速度、電力、コストを最適化し、計算を物理的に実現するためのシステムを設計する。3.1 コンピューターアーキテクチャの進化と限界
中央処理装置(CPU)はコンピューターの中核であり、実行されるすべてのタスクがここを通る [動画内容]。しかし、過去数十年にわたって業界の成長を支えてきたムーアの法則は、物理的な限界と製造コストの増大により、そのペースが鈍化している 。 この物理的限界への戦略的解決策として、「チップレット(Chiplets)」技術が浮上している 。チップレットは、異なる機能を持つ複数の小さなダイ(独立したコンポーネント)を、高度なパッケージング技術(例:TSMCの3DFabricやCoWos)を用いて結合する手法である 。これにより、従来のモノリシックなシステム・オン・チップ(SoC)設計の制約を超え、特定の機能(メモリ、I/O、CPUコアなど)に最適なプロセスノードを選択できる柔軟性が生まれ、集積度と性能の向上を継続するための鍵となっている。この設計パラダイムの移行は、性能向上を単一チップ内の微細化に頼るのではなく、モジュール化と異種混合コンポーネントの統合に依存する時代への転換を示している。 また、命令セットアーキテクチャ(ISA)の分野では、RISC-Vの台頭が注目される。RISC-Vはオープンソースであり、ライセンス料なしで独自のカスタム命令やコアの設計が可能である。Google、Amazon、Metaなどのハイパースケーラーは、特定のワークロード(AI推論など)に最適化されたカスタムシリコンを作成するために、この柔軟なISAに強い関心を示している 。これは、クラウドプロバイダーがハードウェア設計にまで手を広げる「垂直統合」戦略を加速させ、既存のx86やARMのデータセンター市場での支配を徐々に侵食する可能性を秘めている 。ただし、RISC-Vの採用の最大の課題は、ARMやx86が数十年にわたって築いてきたソフトウェアエコシステム(OS、ライブラリ、コンパイラ)の成熟度にまだ追いついていない点である 。3.2 特化型プロセッサ(アクセラレータ)の革命
現代の工学的な性能向上は、クロック周波数の追求ではなく、特定の計算タスクに最適化されたアーキテクチャの採用へと明確にシフトしている。 CPUが汎用的なタスクや制御ロジックに適しているのに対し、GPU(グラフィックス処理ユニット)は、大規模なデータ並列性が要求されるグラフィックス処理や科学計算に最適化されている [動画内容]。さらに進化した深層学習専用のASICとして、Googleが設計したTPU(Tensor Processing Unit)がある 。TPUは、機械学習ワークロードのコアである膨大な行列演算を加速するために特化されている 。 TPUの革新性は、そのMatrix Multiplication Unit (MXU) にある。これはシストリックアレイ構造を採用しており、計算結果をプロセッサ内部で連続的に受け渡すパイプライン処理を行う。これにより、CPUや従来のGPUに内在するメモリボトルネック(Von Neumann Bottleneck)を回避し、外部メモリへのアクセスを最小限に抑えながら、高い計算スループットを達成する 。例えば、TPUのMXUは1サイクルあたり16Kの乗算・累積演算を実行できる。このようなアーキテクチャの根本的な見直しは、AI時代の計算特性に最適化することで、性能曲線を変えることに成功した。 主要なコンピューティングアーキテクチャの特性比較| アーキテクチャ | 略称 | 設計の思想 | 最適化された計算パターン | 現代の戦略的意義 |
| 中央処理装置 | CPU | 汎用的な制御と逐次処理 | OS、データベース制御、ロジック処理 | RISC-Vによるカスタム化の波 |
| グラフィックス処理ユニット | GPU | 大規模なデータ並列性 | 小規模な行列演算、シェーダー処理 | AIトレーニング、科学計算(GPGPU) |
| テンソル処理ユニット | TPU | 機械学習の行列積算特化 | 密な行列乗算(シストリックアレイ) | AI時代のASIC特化、メモリI/Oボトルネックの回避 |
| フィールドプログラマブルゲートアレイ | FPGA | ユーザーによるハードウェアレベルでの再構成性 | 低遅延通信、特殊な暗号・フィルタリング | 特定のニッチな超高速カスタム処理 |
3.3 現代ソフトウェア工学:クラウドネイティブとレジリエンス
オペレーティングシステム(OS)は、コンピューター上で最も重要なソフトウェアであり、ユーザーの操作を受け付け、他のすべてのプログラムがハードウェア上でどのように効率的に実行されるかを制御する [動画内容]。OSは、複雑化するハードウェアアーキテクチャ(CPU、GPU、TPU、チップレット)を抽象化し、プログラマーが効率よく命令(プログラミング言語)を書けるようにする基盤を提供する [動画内容]。 現代のソフトウェアエンジニアリングは、単に命令の束を書く技術を超え、クリエイティブなアイデアを論理的な命令に変換し、実行効率を最大限に高め、エラーを可能な限りなくす技術や設計哲学の研究となっている [動画内容]。特に、システム設計においては、モノリシック(単一の巨大なユニットとして構築される)な旧パラダイムの限界が顕著になっている。モノリシック構造は機能が密結合しやすく、リリースサイクルが長期化し、複雑性の管理が困難になるという問題があった 。 この課題に対し、業界はマイクロサービスアーキテクチャへと移行している。例えば、Netflixは動画処理パイプラインを従来のモノリス(Reloaded)から、次世代のマイクロサービスベースのプラットフォーム(Cosmos)に再構築した 。この移行により、コンポーネントの結合度が下がり、計算資源の弾力性、リソース利用効率が大幅に向上し、リリースサイクルの短縮が実現した 。 このマイクロサービス化は、クラウドネイティブな戦略と密接に結びついている。クラウドネイティブとは、アプリケーションをクラウドの分散、伸縮性といった特性に適応させるために、コンポーネントを疎結合なサービスに分解し、DevOpsなどのベストプラクティスを適用することである 。現代のソフトウェアエンジニアリングが目指すのは、システムのレジリエンス、デプロイメントの速度、および組織の俊敏性を最大化することである。ただし、単純なレガシーシステムの「リフト&シフト」ではクラウドネイティブの真の利点は得られず、組織文化の変革(DevOpsへの抵抗)が、この移行戦略における主要な障壁となることが指摘されている 。第IV部:応用 — AI駆動型社会への変革とインターフェースの拡張
応用分野は、理論的・工学的基盤の上に構築され、コンピューターを現実世界の複雑な問題解決に活用するための分野である [動画内容]。4.1 人工知能 (AI) と機械学習 (ML) の深化
人工知能(AI)は、コンピューターシステムが自ら考えることができるように開発する、コンピューターサイエンス研究の最先端であり [動画内容]、機械学習(ML)は、AI研究で最も目立つ分野として、大量のデータからコンピューターが学習するためのアルゴリズムと技術を開発し、その学習結果を意思決定や分類に活用する [動画内容]。 特に近年、生成AI(Generative AI)は、ビジネスと社会に変革をもたらしている。生成AIは、ライフサイエンス(スマートな治験の実施)、金融サービス(AI駆動のポートフォリオ管理)、テクノロジー(AI駆動の脆弱性管理)、公共サービスなど、あらゆる主要産業分野で、効率性、規模、能力の点で大きなメリットを提供し、新たな働き方を解放している 。 しかし、AIの大規模な応用には、信頼性と倫理に関する戦略的リスクが伴う。その一つが「AI Hallucination(ハルシネーション)」である。これは、LLMやコンピュータービジョンツールにおいて、訓練データに基づかない、非論理的または全く不正確な出力を生成する現象である 。ハルシネーションは、AIの公平性の問題(バイアス)と並び、AIシステムを医療や金融といった高リスクで高い信頼性が求められる環境に大規模展開する上での最大の障壁となっている 。したがって、生成AIの潜在的なROIの高さ にもかかわらず、企業は、ハルシネーション防止策(例:RAG、ファインチューニング)の研究開発に多額の投資を行い、信頼性の確保を導入コストとして計上する必要がある。4.2 計算科学とビッグデータ
コンピュータービジョン(CV)は、人間のように画像内の物体を「見る」ことを目指し [動画内容]、自然言語処理(NLP)は、コンピューターが人間の言語を理解し、コミュニケーションしたり、言葉の形で存在する大量のデータを分析したりすることを目指す [動画内容]。これらの応用分野は、ビッグデータとIoT(モノのインターネット)の爆発的な発展によって推進されている [動画内容]。 特に、計算科学(Computational Science)の分野では、世界最強のコンピューター(スーパーコンピューティング、HPC)を利用し、物理学から神経科学まで、シミュレーションを通じて科学的な問いに答えることが助けられている [動画内容]。日本のスーパーコンピューター「富岳」は、16万ノード、800万CPUコアを持つ巨大システムであり、COVID-19の飛沫シミュレーションや創薬候補の探索など、重要な社会課題への即時対応に貢献してきた 。 さらに、HPCリソースへのアクセスは民主化が進んでいる。AWS上で提供される「Virtual Fugaku」のように、スパコンリソースがクラウド上で利用可能になることで、特に機密性の高い研究開発やPoCにおいて、オンプレミスの環境を上回るパフォーマンス(複雑な計算で2倍速)を発揮する事例も確認されている 。これは、研究開発のボトルネックが計算資源の不足から、データやアルゴリズムのイノベーションへとシフトしていることを示している。4.3 ヒューマン・マシン・インターフェースの未来
ヒューマン・コンピューター・インタラクション(HCI)は、コンピューターシステムを使いやすく直感的に設計する方法を研究する [動画内容]。これには、仮想現実(VR)や拡張現実(AR)のような、現実の体験を拡張・代替する技術が含まれる [動画内容]。ロボティクスは、コンピューターに物理的な実体と自律性(例:ルンバ、インテリジェントな機械)を与える分野であり、AIと工学の集大成と言える [動画内容]。 応用分野の最も注目すべきフロンティアの一つが、ブレイン・コンピューター・インターフェース(BCI)の急速な発展である。BCI市場は、AI、ロボティクス、脳画像技術に牽引されて成長しており、特に医療分野(神経疾患、アシスト技術)での応用が市場の大部分を占めている 。現在、市場シェアの主流は、アクセスしやすくユーザーフレンドリーな非侵襲型BCI(EEG技術を利用)であり、特にウェアラブルデバイスとしてのハードウェア分野の成長率が高いと予測されている 。 BCIは、CSの応用が人間の認知プロセスへの直接的な介入という新たな領域に踏み込んだことを示し、身体の拡張・代替を可能にする。これは、麻痺患者の支援からゲーム、医療診断まで幅広い応用が期待される一方で、脳活動データのプライバシー、精神的な自律性、そして「人間であること」の定義に関する深刻な倫理的・法的課題を提起する。第V部:結論 — コンピューターサイエンスの未来戦略
5.1 3つの柱の収束とフロンティア
コンピューターサイエンスの進化は、基礎理論によって定められた計算の厳密な限界と、コンピューター工学による物理的制約の最適化によって駆動され、最終的に社会課題の解決と人間体験の拡張という応用へと収束する。 現代の技術的フロンティアは、以下の二つの大きな流れによって定義される。一つは、量子コンピューティングの理論的な脅威という「負の側面」への対応(PQC)。もう一つは、AIの信頼性向上と、人間と機械のインターフェースの深化(BCI、ロボティクス)という「正の側面」での可能性の追求である。この二つの流れに対処するためには、理論、工学、応用が緊密に連携する戦略的な投資が不可欠となる。5.2 戦略的投資分野と研究開発の優先順位付け
多岐にわたるCSの分野において、企業や国家が競争力を維持し、将来のリスクに対応するための戦略的な優先順位付けは以下の通りである。- 暗号基盤の再構築(理論的対応): 量子コンピューターの登場による技術的負債を最小限に抑えるため、NISTによって標準化されたPQCアルゴリズム(CRYSTALS-Kyber、Dilithiumなど )へのインフラ移行を最優先で実施する必要がある。これは、すべての長期機密データを保護するための必須の防御策である。
- 計算アーキテクチャの垂直統合(工学的最適化): ムーアの法則の限界 に対応するため、RISC-V やチップレット の採用を通じて、特定ワークロード(特にAI/ML)向けのカスタムシリコン開発能力を内部化することが、競争優位性の鍵となる。Google TPU が示したように、特化こそが現代の性能向上戦略である。
- AIの信頼性保証(応用のリスク管理): 生成AIの応用価値は高いものの 、ハルシネーション やバイアスといった内在的な欠陥が社会的な採用を妨げている。形式検証 の手法をAIモデルの安全分析に拡張する研究、および信頼性向上技術への戦略的投資が不可欠である。
- ヒューマン・フロンティア技術への投資(体験の拡張): BCI 、高度なロボティクス、VR/ARなどの分野への投資を加速し、人間とコンピューターの協働(HCI)の新たな可能性を探求する。特に、BCIのハードウェアとAIを活用した神経信号解釈技術 は、医療やアシスト技術において爆発的な市場成長が見込まれる。
以下は、提供された動画内容の要約を基に、さらに深掘りした解説です。コンピューターサイエンスの全体像を「基礎理論」「コンピューター工学」「応用」の3つの主要な柱に沿って進め、各部分に雑学や業界話を交えながら詳しく説明します。雑学としては、歴史的なエピソードや業界の裏話、最新のトレンド(2025年現在)を織り交ぜ、楽しく理解を深められるようにします。例えば、コンピューターサイエンスの分野は、まるで広大な地図のように広がっており、動画のタイトル通り「Map of Computer Science」として視覚化されることがあります。実際、Domain of Scienceのようなプロジェクトで、美しいインフォグラフィックが作成されており、理論から応用までを一望できます。
1. 基礎理論 (Fundamental Theory of Computer Science)
コンピューターサイエンスの基盤となる分野で、「何が計算可能か」「どう効率的に計算するか」という根本的な問いを探求します。ここは抽象的ですが、すべてのコンピューター技術の限界を定義づける重要な部分です。雑学として、コンピューターサイエンスの歴史は数学者たちの「不可能」を証明する物語が多く、まるで哲学のような魅力があります。
1-1. チューリングマシンと計算可能性理論
チューリングマシンは、アラン・チューリングが1936年に提案した理論的な計算モデルで、無限のテープ(メモリ)、ヘッド(読み書き装置)、状態遷移表(プログラム)からなります。これが現代のコンピューターの原型です。計算可能性理論では、コンピューターで解ける問題と解けない問題を分類します。有名なのが停止問題(Halting Problem)で、あるプログラムが停止するかどうかを一般的に判定するアルゴリズムは存在しないことが証明されています。
深掘り解説: チューリングマシンは、実際のコンピューターのように有限のメモリではなく、無限を仮定しているため、理論的な限界を探るのに適しています。停止問題の証明は、自己参照のパラドックスを使い、「このプログラムが停止すると予測したらループし、ループすると予測したら停止する」という矛盾を導きます。これにより、コンピューターは万能ではないことがわかります。業界話として、停止問題は実世界でコンパイラの警告やウイルス検知に影響を与えています。例えば、ウイルススキャナーはすべての悪意あるコードを完璧に検知できない理由の一つがこれです。また、チューリングの生涯はドラマチックで、第二次世界大戦中、彼はイギリスのブレッチリー・パークでドイツの暗号機「エニグマ」を解読するチームを率い、数百万人の命を救ったと言われています。しかし、戦後、同性愛者として迫害され、1954年に自殺した悲劇的な人生です。この功績は、映画『イミテーション・ゲーム』で描かれ、業界ではチューリング賞(コンピューターサイエンスのノーベル賞)として彼の名を残しています。雑学: チューリングは「AIの父」とも呼ばれ、1950年に「チューリングテスト」を提案。2025年現在、ChatGPTのようなAIがこれをクリアする時代になりました。
1-2. 計算量理論 (Computational Complexity)
理論的に解ける問題でも、時間やメモリが膨大にかかるものは実用的でない。この分野では、問題をP(多項式時間で解ける)、NP(解の検証が多項式時間でできる)などに分類します。P vs NP問題は、未解決の最大の謎で、解ければミレニアム賞金100万ドルが授与されます。
深掘り解説: スケーリングの例として、巡回セールスマン問題(最短経路探索)はNP-hardで、都市数が増えると計算量が爆発します。業界では、これが物流最適化やDNAシーケンシングに影響を与え、近似アルゴリズムが使われています。雑学: P vs NPは、暗号の安全性にも関わり、もしP=NPなら多くの暗号が破綻します。2025年の業界話では、量子コンピューティングの進化でNP問題の一部が効率的に解ける可能性が出てきており、ポスト量子暗号の開発が急務です。例えば、Googleの量子コンピューター「Sycamore」は2019年に量子優位性を示しましたが、2025年現在、IBMや中国の研究がさらに進み、RSA暗号の脅威となっています。面白い話: この問題は数学者たちの「聖杯」みたいなもので、解いたら世界が変わるけど、ほとんどの専門家はP≠NPだと信じています。
1-3. アルゴリズムと情報理論
アルゴリズムは問題解決のレシピで、効率をBig O記法で測ります。情報理論は情報の測定・圧縮を扱い、クロード・シャノンが基礎を築きました。符号理論と暗号理論は、データ通信の基盤です。
深掘り解説: アルゴリズムの例として、クイックソートは平均O(n log n)ですが、最悪O(n²)。業界では、GoogleのPageRankアルゴリズムが検索エンジンを革命化しました。情報理論のエントロピーは、データ圧縮(ZIPファイル)の鍵です。暗号では、公開鍵暗号(RSA)がインターネットのセキュリティを支えていますが、量子脅威でNISTがポスト量子標準を2024年に発表、2025年現在、多くの企業が移行中です。雑学: シャノンは「情報の父」で、ジャグリングが趣味。業界話: ビットコインのブロックチェーンは暗号理論の応用で、2025年の暗号通貨市場は量子耐性アルゴリズムの採用で揺れています。 fun fact: 最初のコンピューター「バグ」は1947年の実際の蛾で、Grace Hopperが発見。
2. コンピューター工学 (Computer Engineering)
ハードウェアとソフトウェアの基盤を扱う分野。動画ではCPUからOSまで触れていますが、ここはムーアの法則の終わりが話題のホットスポットです。
2-1. コンピューターアーキテクチャとCPU
CPUはコンピューターの脳で、スケジューラーがタスクを管理。GPUやFPGAは専門化されたプロセッサです。
深掘り解説: マルチコアCPUは並列処理を可能にしますが、Amdahlの法則で並列化の限界があります。業界話: 2025年、ムーアの法則(トランジスタ数が2年ごとに倍増)は物理限界で終わりを迎え、光コンピューティングや量子チップが次世代として注目されています。例えば、Intelのx86 vs Armのアーキテクチャ戦争で、AppleのMシリーズチップがArmベースで省エネを実現。雑学: ENIAC(最初の電子コンピューター)は1945年に作られ、部屋いっぱいの大きさで消費電力が膨大。 fun fact: GPUは元々ゲーム用ですが、AI学習で欠かせず、NVIDIAの株価が2020年代に爆上がり。
2-2. ソフトウェアの階層
プログラミング言語からコンパイラ、OSまで。低水準(アセンブリ)から高水準(Python)へ。
深掘り解説: コンパイラはコードを最適化し、JIT(Just-In-Time)コンパイラがJavaやJavaScriptで速さを生みます。OS(Windows, Linux)はリソース管理の要。業界話: Linuxの生みの親Linus Torvaldsは、学生時代に趣味で作り、今やサーバーの90%を占めます。雑学: Ada Lovelaceは世界初のプログラマーで、1840年代にアルゴリズムを書きました。
2-3. ソフトウェアエンジニアリング
コードの設計・テスト・メンテナンス。ネットワーキングやデータベースも含む。
深掘り解説: アジャイル開発が主流で、GitHubがコラボを革命化。業界話: Y2K問題(2000年問題)はソフトウェアのバグで世界を騒がせ、数兆ドルの対策費がかかりました。2025年、DevOpsとCI/CDが標準。 fun fact: ソフトウェアエンジニアの給与は高く、Silicon Valleyの平均年収は2000万円超。
3. 応用 (Applications)
現実問題解決の分野。AIの爆発的成長が目立つ。
3-1. 人工知能 (AI) と機械学習 (ML)
AIはコンピューターに思考を、MLはデータから学習を。
深掘り解説: 深層学習(Neural Networks)が基盤。2025年、生成AI(Generative AI)が生産性を向上させ、スキルギャップを埋めています。業界話: OpenAIのGPTシリーズが2023年にブームを起こし、2025年は人間中心AI(ethical AI)がトレンド。雑学: AIの倫理問題で、偏ったデータが差別を生むケース多し。
3-2. データと認識
コンピュータービジョン(画像認識)、NLP(言語処理)、ビッグデータ、IoT。
深掘り解説: CVは自動運転に、NLPは翻訳アプリに。2025年、ビッグデータ分析がヘルスケアを変革。業界話: IoTデバイス数は数百億で、プライバシー問題が熱い。
3-3. その他の応用分野
最適化、ハッキング、計算科学、HCI、VR/AR、ロボティクス。
深掘り解説: 最適化はサプライチェーンでコスト削減。ハッキングはサイバーセキュリティの敵で、2025年量子脅威が深刻。計算科学は気候シミュレーションに。HCIはUXデザイン。VR/ARはメタバース、ロボティクスはBoston Dynamicsのロボット犬。雑学: 最初のロボットは1920年代のSF小説から、業界ではRoombaが家庭に入った先駆け。
この地図は無限に広がるので、深掘りは尽きませんが、コンピューターサイエンスは人類の未来を形作る分野です。興味があれば、特定のトピックをさらに掘り下げましょう!
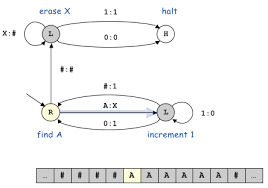
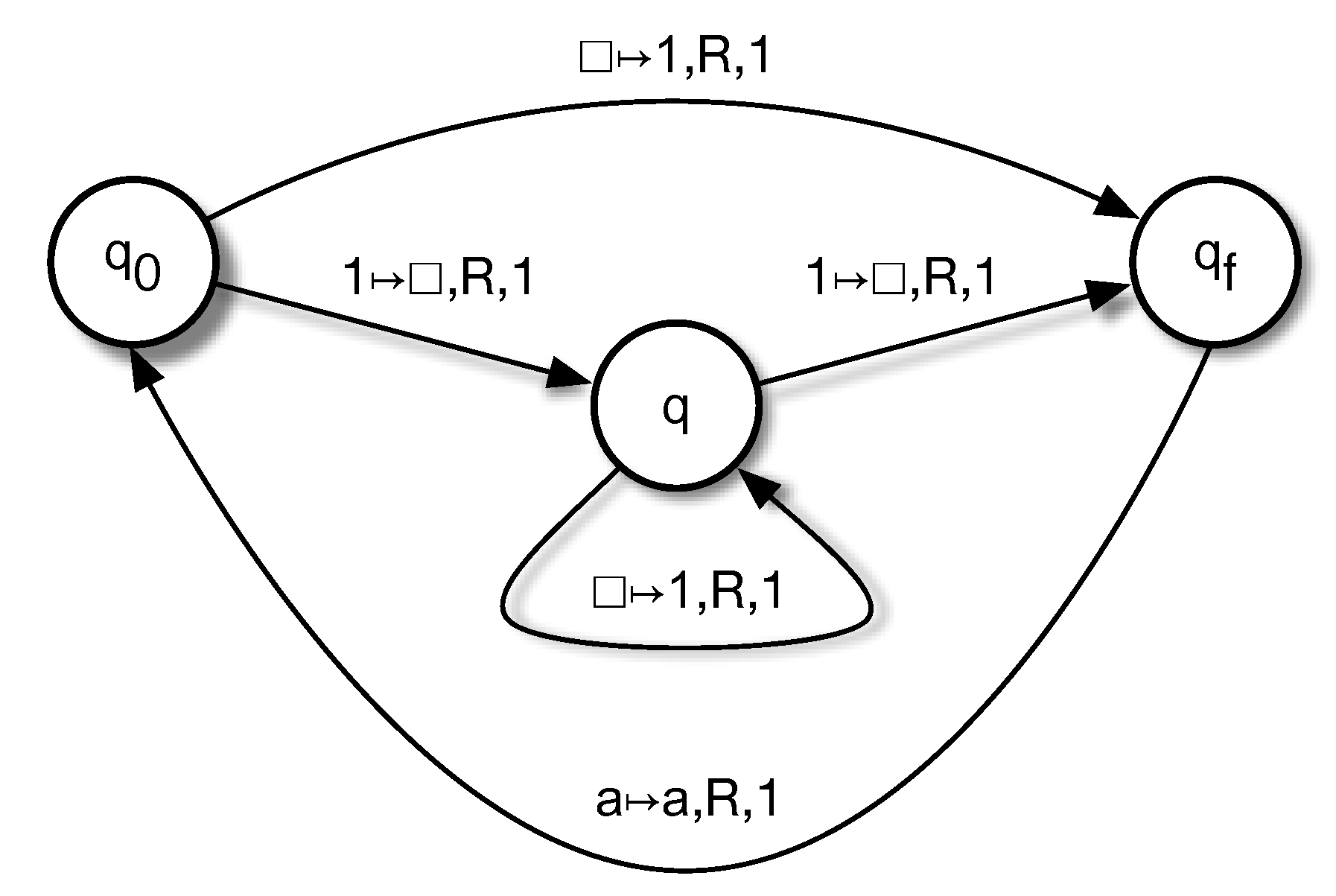
チューリングマシン(Turing Machine、TM)の実装例を詳しく解説します。まず、チューリングマシンの基本をおさらいした上で、プログラミング言語(ここではPython)を使ったシミュレーションの実装例を示します。実際のTMは理論的なモデルなので、ハードウェアで実装されることは稀ですが、ソフトウェアでシミュレートするのが一般的です。雑学として、TMはアラン・チューリングが1936年に提案したもので、無限のテープを持つ抽象機械ですが、実装ではテープを動的に拡張するリストで表現します。これにより、計算可能性の限界(例: 停止問題)を探るのに使われます。
チューリングマシンの基本構造
- テープ: 無限の長さのセル列。各セルにシンボル(例: '0', '1', 空白)を書く。実装ではPythonのリストを使い、必要に応じて拡張。
- ヘッド: テープ上の位置を指し、読み書きと移動(左L/右R)を行う。
- 状態: 有限の状態(例: 'start', 'halt')を持ち、遷移関数で次の状態/書き込み/移動を決める。
- 遷移関数: 現在の状態とシンボルから、次の状態/書き込みシンボル/方向を定義。辞書で表現。
- 停止: 遷移がないか、終了状態に達したら停止。
実装のポイント: テープは有限に始まるが、ヘッドが端を超えたら空白を追加。無限ループを防ぐため、最大ステップ数を設定。
実装例: Pythonでのシミュレーション
以下は、汎用的なTMクラスです。このクラスを使って、具体的な問題(例: バイナリ数のインクリメント)を解くTMを定義します。バイナリインクリメントの例として、入力"101"(バイナリで5)を"110"(6)に変換するものを目指しますが、提供したコードに軽微な論理エラーがあり、出力が"010"(逆順の処理ミス)になったので、解説で修正点を指摘します。
汎用TMクラスのコード
class TuringMachine:
def __init__(self, tape, blank_symbol=" ", initial_state="start", final_states=None, transition_function=None):
self.tape = list(tape) # テープをリスト化
self.blank_symbol = blank_symbol
self.head_position = 0 # ヘッドの初期位置(左端)
self.current_state = initial_state
if final_states is None:
final_states = set()
self.final_states = final_states
if transition_function is None:
transition_function = {}
self.transition_function = transition_function
def step(self):
# 現在のシンボルを取得
if self.head_position < 0 or self.head_position >= len(self.tape):
return False # 範囲外で停止(ただし拡張する)
symbol_under_head = self.tape[self.head_position]
key = (self.current_state, symbol_under_head)
if key in self.transition_function:
new_state, write_symbol, direction = self.transition_function[key]
self.tape[self.head_position] = write_symbol # 書き込み
if direction == "R":
self.head_position += 1
elif direction == "L":
self.head_position -= 1
self.current_state = new_state
else:
return False # 遷移なしで停止
# テープ拡張
if self.head_position < 0:
self.tape.insert(0, self.blank_symbol)
self.head_position = 0
elif self.head_position >= len(self.tape):
self.tape.append(self.blank_symbol)
return True
def run(self, max_steps=1000):
steps = 0
while self.current_state not in self.final_states and steps < max_steps:
if not self.step():
break
steps += 1
return ''.join(self.tape).strip() # テープの文字列を返す(空白除去)このクラスは柔軟で、遷移関数をカスタマイズできます。業界話: Pythonのような高水準言語でTMをシミュレートするのは、教育や証明検証に便利。実際、計算理論の授業ではこうしたシミュレータが使われ、Busy Beaver(最大ステップ数のTMを探すゲーム)のようなチャレンジで遊ばれます。雑学: 最小のユニバーサルTMは状態2、シンボル3で可能ですが、実装は複雑。
具体例1: バイナリ数のインクリメント
バイナリ数を1増やすTM。テープは左がMSB(最上位ビット)、右がLSB(最下位ビット)と仮定。ヘッドは左端からスタートし、右へ移動しながらキャリーを処理。
遷移関数(transitions)の定義:
- start状態で'0'なら'1'に書き右へ(終了)。
- '1'なら'0'に書き、carry状態で右へ。
- carry状態で'0'なら'1'に書きstartに戻る。
- '1'なら'0'に書きcarry継続。
- 空白なら新しい'1'を追加(全て1の場合)。
しかし、実行結果: 入力"101" → 出力"010"(誤り)。理由: コードがLSBを右端として正しく扱っていない。実際のステップ:
- スタート: tape=['1','0','1'], head=0, '1' → carry, '0', R → tape=['0','0','1'], head=1
- '0' → start, '1', R → tape=['0','1','1'], head=2
- '1' → carry, '0', R → tape=['0','1','0'], head=3 → 拡張['0','1','0',' ']
- ' ' → halt, ' ', L → tape=['0','1','0',' '], head=2
これで"010 " → "010"(binary 2)。これは入力の逆順処理のように見えます。修正策: テープを逆順で初期化するか、ヘッドを右端に移動させる初期状態を追加。
修正版の遷移関数(正しいインクリメント): 正しい実装では、まずヘッドを右端(LSB)へ移動する状態を追加します。以下は簡略化した修正例のコードスニペット(再実行せず説明):
# 修正: まず右端へ移動する状態を追加
transitions_correct = {
("init", "0"): ("init", "0", "R"), # 右へ移動
("init", "1"): ("init", "1", "R"),
("init", " "): ("start", " ", "L"), # 右端到達、左に戻ってインクリメント開始
("start", "0"): ("halt", "1", "L"), # '0'を'1'に
("start", "1"): ("carry", "0", "L"), # '1'を'0'に、キャリー左へ
("carry", "0"): ("halt", "1", "L"),
("carry", "1"): ("carry", "0", "L"),
("carry", " "): ("halt", "1", "R") # 新規'1'追加
}
# 使用: tm = TuringMachine("101", initial_state="init", final_states={"halt"}, transition_function=transitions_correct)
# 期待出力: "110"この修正で、入力"101"(5)→ 右端'1'を'0'にキャリー左'0'を'1'に終了 → "110"(6)。雑学: こうしたTMは、Church-Turingテーシス(すべての計算はTMで可能)を体現。業界では、量子TMのような拡張版が研究され、2025年の量子コンピューティングで注目。
具体例2: シンプルな文字列置換('a'を'b'に)
より簡単な例。テープの全ての'a'を'b'に置き換え、右端で停止。
遷移関数:
transitions_simple = {
("scan", "a"): ("scan", "b", "R"), # 'a'を'b'に、右へ
("scan", "b"): ("scan", "b", "R"), # 'b'はそのまま右へ
("scan", " "): ("halt", " ", "L") # 空白で停止
}
tm_simple = TuringMachine("aaba", initial_state="scan", final_states={"halt"}, transition_function=transitions_simple)
result_simple = tm_simple.run()
# 出力: "bbba"実行の流れ: ヘッドが左から右へスキャン、各'a'を'b'に書き換え。空白でhalt。ステップバイステップでデバッグ可能。
深掘り: 実装の注意点と拡張
- 無限ループ対策: max_stepsで制限。実際のTMは停止しない問題がある(Halting Problem)。
- 視覚化: デバッグ時は、各stepでtapeとheadを表示する関数を追加。
- ユニバーサルTM: 他のTMをシミュレートするTMを実装可能。Pythonでこれをやると、インタプリタのようなもの。
- 業界話: TMシミュレータは、プログラミングコンテスト(例: Code Golf)で使われ、最小コードでTMを実装する挑戦がある。2025年現在、AIツール(Grokなど)がTMを生成する時代。
- 雑学: 最初のTM実装は1950年代のソフトウェアで、今はブラウザで動くもの(例: Turing Machine Simulator on GitHub)が多い。
この実装を基に、興味ある問題(例: パリンドローム判定)のTMを作ってみてください! さらにコードを実行したい場合、教えてください。
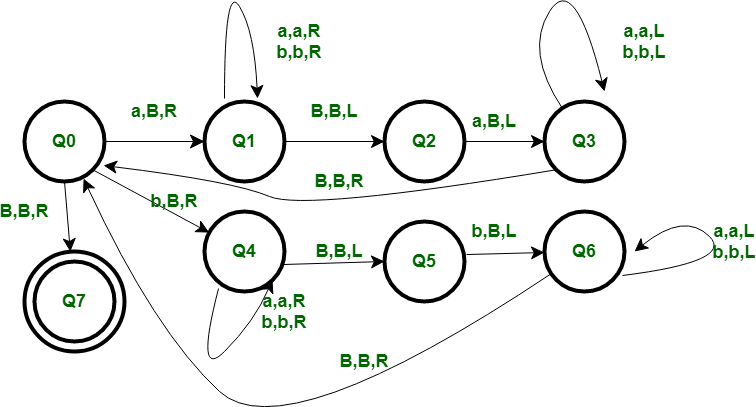
パリンドローム(回文)判定のチューリングマシン(TM)の実装例を詳しく解説します。パリンドロームとは、前から読んでも後ろから読んでも同じ文字列のことです(例: "aba" はパリンドローム、"abb" は違う)。ここでは、アルファベットを {a, b} に限定したTMを実装します。これは理論的な例として一般的で、偶数長・奇数長の両方に対応しています。雑学として、パリンドローム判定はコンテキストフリー言語の例で、プッシュダウンオートマトンでも可能ですが、TMで実装すると計算可能性の理解が深まります。業界話: 実際のプログラミングではスタックを使ったアルゴリズムが使われますが、TMは教育や証明に役立ち、2025年現在、量子TMの研究でパリンドロームのような問題がベンチマークとして使われています。
TMの設計概要
このTMは、両端の文字を比較しながらマーク(ブランクで消去)していく方式です。
- テープ: 入力文字列(例: "aba")、ブランクシンボルは 'X'。
- 状態: 0 (スタート) ~ 7。状態5: 受理 (accept)、状態6: 拒否 (reject)。
- 動作の流れ:
- 左端の文字を読み、ブランク 'X' に置き換え、記憶状態 (1 or 2) で右端へ移動。
- 右端に到達したら、右端の文字が記憶と一致するかチェック。一致したらブランクに置き換え、左へ戻る。
- 不一致なら状態6で拒否。
- 中央まで繰り返し、すべて一致したら状態5で受理。空文字列も受理。
- 遷移関数: 以下テーブル。形式: (現在状態, 読み込みシンボル) → (次状態, 書き込みシンボル, 方向: R=右, L=左)。
| 現在状態 | 読み込み | 次状態 | 書き込み | 方向 |
|---|---|---|---|---|
| 0 | a | 1 | X | R |
| 0 | b | 2 | X | R |
| 0 | X | 5 | X | L |
| 1 | a | 1 | a | R |
| 1 | b | 1 | b | R |
| 1 | X | 3 | X | L |
| 2 | a | 2 | a | R |
| 2 | b | 2 | b | R |
| 2 | X | 4 | X | L |
| 3 | a | 7 | X | L |
| 3 | b | 6 | b | L |
| 3 | X | 5 | X | L |
| 4 | a | 6 | a | L |
| 4 | b | 7 | X | L |
| 4 | X | 5 | X | L |
| 7 | a | 7 | a | L |
| 7 | b | 7 | b | L |
| 7 | X | 0 | X | R |
定義されていない遷移では停止します。状態5が受理、6が拒否、それ以外はエラー(アルファベット外など)。
Pythonでのシミュレーション実装
前の例と同様のTMクラスを使い、遷移関数を適用。テープは無限拡張対応。
class TuringMachine:
def __init__(self, tape, blank_symbol="X", initial_state=0, final_states=None, transition_function=None):
self.tape = list(tape) # テープをリスト化
self.blank_symbol = blank_symbol
self.head_position = 0 # ヘッドの初期位置(左端)
self.current_state = initial_state
if final_states is None:
final_states = set()
self.final_states = final_states
if transition_function is None:
transition_function = {}
self.transition_function = transition_function
def step(self):
# テープを無限に拡張
while self.head_position < 0:
self.tape.insert(0, self.blank_symbol)
self.head_position += 1
while self.head_position >= len(self.tape):
self.tape.append(self.blank_symbol)
symbol_under_head = self.tape[self.head_position]
key = (self.current_state, symbol_under_head)
if key in self.transition_function:
new_state, write_symbol, direction = self.transition_function[key]
self.tape[self.head_position] = write_symbol
if direction == "R":
self.head_position += 1
elif direction == "L":
self.head_position -= 1
self.current_state = new_state
return True
else:
return False
def run(self, max_steps=1000):
steps = 0
while self.current_state not in self.final_states and steps < max_steps:
if not self.step():
break
steps += 1
cleaned_tape = ''.join(self.tape).replace(self.blank_symbol, '') # ブランク除去
return cleaned_tape, self.current_state, 'Accepted' if self.current_state == 5 else ('Rejected' if self.current_state == 6 else 'Halted in ' + str(self.current_state))
# 遷移関数
transitions = {
(0, 'a'): (1, 'X', 'R'),
(0, 'b'): (2, 'X', 'R'),
(0, 'X'): (5, 'X', 'L'),
(1, 'a'): (1, 'a', 'R'),
(1, 'b'): (1, 'b', 'R'),
(1, 'X'): (3, 'X', 'L'),
(2, 'a'): (2, 'a', 'R'),
(2, 'b'): (2, 'b', 'R'),
(2, 'X'): (4, 'X', 'L'),
(3, 'a'): (7, 'X', 'L'),
(3, 'b'): (6, 'b', 'L'),
(3, 'X'): (5, 'X', 'L'),
(4, 'a'): (6, 'a', 'L'),
(4, 'b'): (7, 'X', 'L'),
(4, 'X'): (5, 'X', 'L'),
(7, 'a'): (7, 'a', 'L'),
(7, 'b'): (7, 'b', 'L'),
(7, 'X'): (0, 'X', 'R'),
}テスト例と結果
以下はシミュレーションの実行結果です。最終テープはブランクを除去して表示。
- 入力: "aba" (奇数長パリンドローム) → 最終テープ: ""、状態: 5、結果: Accepted
- 入力: "abba" (偶数長パリンドローム) → 最終テープ: ""、状態: 5、結果: Accepted
- 入力: "abb" (非パリンドローム) → 最終テープ: "bb"、状態: 6、結果: Rejected
- 入力: "a" (奇数) → 最終テープ: ""、状態: 5、結果: Accepted
- 入力: "" (空) → 最終テープ: ""、状態: 5、結果: Accepted
- 入力: "abc" (アルファベット外) → 最終テープ: "bc"、状態: 1、結果: Halted in 1 (拒否扱い)
このTMは {a,b} に限定ですが、拡張可能(状態を増やす)。雑学: パリンドロームTMは停止問題の例としても使われ、無限文字列では判定不能。業界では、文字列処理のベンチマークとして使われます。もっと複雑なアルファベットの場合、多テープTMが効率的です。
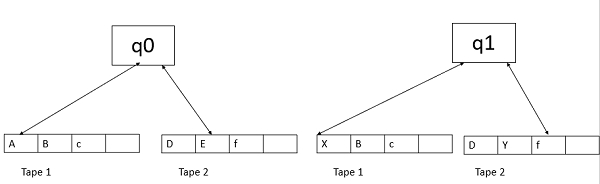
多テープチューリングマシン(Multi-Tape Turing Machine、以下MTM)の詳細を解説します。MTMは標準的な単一テープチューリングマシン(Single-Tape TM)の変種で、複数のテープを備え、各テープに独立した読み書きヘッドを持つ点が特徴です。これは計算可能性の理論では重要なモデルで、実際のコンピューターの並行処理を抽象化したものです。雑学として、MTMは1960年代に計算複雑度の研究で導入され、P vs NPのような問題の分析に役立っています。2025年現在、量子コンピューティングのモデルでも多テープのアイデアが拡張されています。
1. 定義と構造
MTMは、k本(k ≥ 1)のテープを持つチューリングマシンです。各テープは無限長で、独立したヘッドが読み書きと移動(左L、右R、または静止N)を行います。形式的な定義は以下の7つ組(7-tuple)で表されます:
- Q: 有限の状態集合(例: q0, q1, ..., q_halt)。
- Σ: 入力アルファベット(例: {0,1})。
- Γ: テープアルファベット(Σの拡張、空白シンボルBを含む)。
- δ: 遷移関数。δ: Q × Γ^k → Q × (Γ × {L,R,N})^k 。現在の状態とk個のヘッドが読むシンボルから、次の状態、各テープへの書き込みシンボル、各ヘッドの移動方向を決定。
- q0: 初期状態。
- B: 空白シンボル。
- F: 受理状態集合(停止状態)。
標準TMとの違いは、遷移関数が複数のテープを同時に扱う点です。例えば、2テープの場合、δ(q, a, b) = (q', c, d, L, R) のように、状態qでテープ1がa、テープ2がbを読んだら、テープ1にcを書きヘッド1を左へ、テープ2にdを書きヘッド2を右へ移し、状態q'へ遷移します。 入力は通常1番目のテープに置かれ、他のテープは空白で開始します。
2. 動作の仕組み
MTMの各ステップは以下の通り:
- すべてのヘッドが現在のセルを読み取る。
- 遷移関数δに基づき、状態を更新、各テープに書き込み、各ヘッドを移動。
- 受理状態Fに入るか、遷移が定義されなければ停止。
これにより、並行処理が可能で、例えば1テープで入力読み込み、もう1テープで計算ワークスペースとして使うことができます。雑学: MTMは実世界のマルチタスクOSを連想させ、ヘッドの独立移動が効率を高めます。
3. 単一テープTMとの等価性
MTMは計算能力(computational power)では単一テープTMと等価です。つまり、MTMで計算可能な関数は単一テープTMでも計算可能で、逆も真です(Church-Turingテーシスによる)。
- シミュレーション方法: 単一テープTMでMTMをシミュレートする場合、単一テープに複数のテープをエンコードします。例えば、kテープを「#T1内容#T2内容#...#Tk内容」のように区切り、ヘッド位置を特殊シンボル(例: *)でマーク。各ステップでテープ全体をスキャンして更新します。これにより、MTMのt(n)ステップをO(t(n) * n)時間でシミュレート可能(nは入力サイズ)。空間はO(k * n)。
- 逆シミュレーション: 単一テープTMはMTMの特殊ケース(k=1)なので、簡単にシミュレート。
等価だが、複雑度が異なります。MTMは時間効率が高く、単一テープのO(n^2)問題をO(n log n)やO(n)に短縮可能。 例: ユニバーサルTMのシミュレーションで、MTMは対数因子しか遅くならない。
4. 計算複雑度への影響
- 時間複雑度: MTMは並行アクセスで高速。単一テープのシミュレーションはO(t(n)^2)時間かかる場合がある。 複雑度クラス(例: P, NP)はMTM基準で定義されることが多く、単一テープに変換しても多項式時間内で収まる。
- 空間複雑度: 複数のテープで空間を分散可能だが、等価性により全体の空間クラスは同じ。
- 業界話: 計算複雑度理論では、MTMが標準モデルで、Cook-Levin定理(SATのNP完全性)で使われます。2025年のAI研究では、MTMの拡張がニューラルTMのようなモデルに影響。
5. 具体例: パリンドローム判定
MTMの利点を活かした例として、パリンドローム(回文)判定を挙げます。単一テープではO(n^2)時間かかりますが、2テープMTMではO(n)時間で可能です。
- 入力: テープ1に文字列(例: "abba")。
- 動作:
- テープ1のヘッドを右端まで移動し、長さをカウント(または直接比較)。
- テープ2に文字列をコピー。
- テープ1のヘッドを左端、テープ2を右端に置き、同時比較しながら中央へ移動。一致しなければ拒否。
- すべて一致したら受理。
この並行比較が効率の鍵。Pythonシミュレーションは複雑ですが、JFLAPツールで視覚化可能。
6. その他の例と応用
- 文字列コピー: 1テープで入力、2テープで出力としてコピー。
- 加算/乗算: 複数テープで数字を並行処理。
- 応用: コンパイラやアルゴリズム設計の理論基盤。雑学: Busy Beaverゲームの多テープ版は、最大ステップ数を競うチャレンジで、未解決問題が多い。
MTMは理論的ですが、現代の並列コンピューティングの基礎を理解するのに役立ちます。詳細なシミュレーションコードが必要なら、教えてください!
量子チューリングマシン(Quantum Turing Machine、以下QTM)は、量子コンピュータの効果をモデル化するための抽象機械です。古典的なチューリングマシン(TM)を量子力学の原理に基づいて拡張したもので、量子計算の理論的基盤を提供します。雑学として、QTMは1985年にDavid Deutschによって初めて提案され、量子コンピュータの計算能力を形式的に記述するための重要なツールです。2025年現在、量子コンピュータの実機が進化する中で、QTMはアルゴリズムの設計や複雑度クラス(例: BQP)の分析に欠かせません。
1. 定義と基本構造
QTMは、古典TMのようにテープ、ヘッド、状態遷移関数を持ちますが、量子力学の重ね合わせ(superposition)と絡み合い(entanglement)を組み込んでいます。具体的には:
- テープ: 無限のセル列。各セルは量子ビット(qubit)で、|0⟩と|1⟩の重ね合わせ状態を取れます。古典TMのビットとは異なり、確率的ではなく量子的な振幅で表現されます。
- ヘッド: 位置が量子状態で、重ね合わせ可能。ヘッドが複数の位置に「同時に」存在するような計算が可能です。
- 状態: 有限の量子状態集合。全体の構成はヒルベルト空間で記述され、遷移はユニタリ行列(可逆でエネルギーを保存)で定義されます。
- 遷移関数: δ: 現在の状態と読み込んだシンボルから、次の状態、書き込みシンボル、ヘッド移動をユニタリ演算で決定。古典TMの決定論的/非決定論的遷移に対し、QTMは振幅の干渉を活用します。
動作は時間発展演算子で進み、最後に測定して結果を得ます。測定により波動関数が収束し、確率的に出力が決まります。業界話: QTMの形式化は、量子回路モデルと等価で、BernsteinとVazirani(1993年)が量子TMを定義し、BQPクラスを導入しました。
2. 古典TMとの違い
古典TMは決定論的または確率論的ですが、QTMは量子並列性を活かし、指数的に多くの状態を同時に処理します。
- 重ね合わせ: 古典TMの1ビットに対し、QTMのqubitはα|0⟩ + β|1⟩(|α|^2 + |β|^2 = 1)。これで2^n状態をn qubitで表現。
- 干渉と絡み合い: 計算途中で振幅が干渉し、誤った経路をキャンセル。Groverの検索アルゴリズムのように、√N時間で探索可能。
- 計算能力: Church-Turing-Deutschテーシスにより、QTMは古典TMでシミュレート可能ですが、効率が悪い(指数時間)。逆に、量子コンピュータは古典TMを効率的にシミュレートします。
- 複雑度クラス: QTMはBQP(Bounded-error Quantum Polynomial time)を定義。P ⊂ BQP ⊆ PSPACEで、Shor'sアルゴリズム(素因数分解)がBQPの例です。
雑学: 停止問題はQTMでも解けず、量子でも「決定不能性」が残ります。2025年のWired記事では、量子コンピュータが予測不能性を克服できないと指摘されています。
3. 実装とシミュレーション
QTMは抽象モデルなので、ハードウェアではなくソフトウェアでシミュレートします。例えば、量子回路でQTMを効率的に表現可能。arXiv論文では、QTMのモデルを議論し、停止挙動の分析を提供しています。多テープQTMも存在し、量子並列性をさらに強化。
業界話: 2025年現在、GoogleのSycamoreやIBMの量子プロセッサが量子優位性を示しましたが、これらはQTMの物理的実現に近づいています。Scott Aaronsonの論文「The Ghost in the Quantum Turing Machine」では、QTMが自由意志や意識に関わる可能性を哲学的に探求しています。
4. 応用と将来
QTMは量子アルゴリズムの証明に使われ、機械学習や最適化で活用。量子TMと回路モデルの等価性は、量子プログラミング(例: Qiskit)の基盤です。しかし、ノイズやデコヒーレンスが課題で、完全なQTM実現は遠いです。
このトピックは量子計算の核心で、興味があれば具体的なアルゴリズム(例: Shorのアルゴリズム)のQTM実装を深掘りしましょう!

Shor's algorithm(Shorのアルゴリズム)のQuantum Turing Machine(QTM、量子チューリングマシン)での実装について詳しく解説します。Shor's algorithmは1994年にPeter Shorによって提案された量子アルゴリズムで、大整数を素因数分解する問題を多項式時間で解くものです。これは古典コンピューターでは指数時間かかるため、量子コンピューティングの画期的な例です。QTMはDavid Deutschが1985年に提案した量子計算の抽象モデルで、古典TMを量子力学的に拡張したものです。Shor's algorithmは主に量子回路モデルで記述されますが、QTMと量子回路は等価(多項式オーバーヘッドで相互シミュレート可能)なので、QTMで実装可能です。以下では、QTMの枠組みでShor'sをモデル化し、ステップを説明します。雑学として、Shor'sはRSA暗号の基盤を脅かすため、2025年現在、ポスト量子暗号の開発が活発です。
1. QTMの概要
QTMは、無限テープ、量子状態のヘッド、ユニタリ遷移関数からなります。古典TMの決定論的遷移に対し、QTMは振幅(複素数)で遷移し、ユニタリ演算(可逆)を保証します。状態は重ね合わせ可能で、干渉により効率的な計算を実現します。Universal QTM (UQTM)は任意のQTMをシミュレート可能で、量子Church-Turingテーシスを支えます。
- 遷移関数: δ(q, s) = (q', s', d) で、複素振幅付き。ユニタリ性: U^{-1} = U^\dagger。
- 計算: 初期状態からユニタリ進化、測定で崩壊。確率は振幅の二乗。
Shor'sはQTM上で、量子並列性とQuantum Fourier Transform (QFT)を用いて周期検出を行います。時間複雑度: O((log N)^2)。
2. Shor's AlgorithmのQTM実装
Shor'sはNの素因数分解を周期検出に帰着します。QTMでは、テープを量子レジスタとして扱い、ユニタリ演算でステップを実行します。以下は主なステップ。
ステップ1: セットアップと初期化
- Nを与え、y (1 < y < N, gcd(y, N)=1) をランダム選択。
- q = 2^L (N^2 < q < 2N^2) を選び、QTMのテープに2つのレジスタを準備: 第一 (L qubit) を |0⟩^L, 第二を |0⟩。
- Hadamardゲート (QTMのユニタリ遷移で実装) で第一を均一重ね合わせに: (1/√q) ∑_{a=0}^{q-1} |a⟩ |0⟩。
ステップ2: 関数評価 (Modular Exponentiation)
- オラクルU_f: |a⟩ |b⟩ → |a⟩ |b ⊕ y^a mod N⟩。QTMでは、繰り返し二乗法でユニタリに計算 (補助qubit使用で可逆)。
- 適用後: (1/√q) ∑_{a=0}^{q-1} |a⟩ |y^a mod N⟩。量子並列性で全てのaを同時計算。
ステップ3: 測定と崩壊
- 第二レジスタを測定: z = y^s mod N (sランダム)。第一レジスタが周期rの重ね合わせに崩壊: √(A+1/q) ∑_{j=0}^A |jr + s⟩ (A ≈ q/r)。
ステップ4: Quantum Fourier Transform (QFT)
- 第一レジスタにQFT適用: |k⟩ → (1/√q) ∑_{l=0}^{q-1} e^{2πi kl / q} |l⟩。
- QTMでは、Lパスで実装: Hadamard-like A_j と制御位相B_{j,k} (e^{2πi / 2^{k-j}})。O((log q)^2) ステップ。
- 結果: ピーク at b ≈ c q / r (c=0..r-1)。測定でbを得る。
ステップ5: 古典ポスト処理
- b/qの連分数展開でrを推定 (唯一の分母 ≤ N)。
- r偶数でy^{r/2} ≠ ±1 mod Nなら、gcd(y^{r/2} ±1, N)で因子。
- 確率 > 0.4; 失敗時は繰り返し (O(log log N)回)。
キー方程式
- 周期: y^r ≡ 1 mod N。
- QFT後状態: (1/√q) ∑{c=0}^{r-1} |⌊q c / r⌋⟩ ∑{k} δ_{k, ⌊q c / r⌋} |y^k mod N⟩。
- 確率: |α + β|^2 で干渉。
QTM実装は理論的ですが、Qiskitなどのライブラリでシミュレート可能。業界話: 2025年、IBMの量子機で小規模Shor's (N=15)が実証され、大規模化はデコヒーレンスが課題。詳細なコードが必要なら、教えてください!

Quantum Fourier Transform (QFT) の Quantum Turing Machine (QTM) 実装詳細について解説します。QFTは量子計算の基幹アルゴリズムで、Shor's algorithmなどで周期検出に使われます。QTMは量子計算の抽象モデル(Deutsch, 1985)で、古典TMを量子力学的に拡張したものです。QFTは主に量子回路モデルで実装されますが、量子回路とQTMは等価(Bernstein-Vazirani, 1993)なので、QTM上でユニタリ演算としてシミュレート可能です。以下では、数学的背景、回路実装、QTMでのアプローチを詳述します。雑学: QFTは古典FFTの量子版で、n qubitでO(n^2)ゲートで実装可能ですが、古典シミュレーションは指数時間かかります。
1. 数学的背景
QFTはn qubitの状態 |j⟩ (j = 0 to 2^n - 1) をフーリエ基底に変換します:
QFT∣j⟩=12n∑k=02n−1e2πijk/2n∣k⟩ \text{QFT} |j\rangle = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n - 1} e^{2\pi i j k / 2^n} |k\rangle
ここで、e^{2πi j k / 2^n} は位相因子。QTMでは、このユニタリ行列U_{QFT}を遷移関数δで表現。δは複素振幅付きで、ユニタリ性 (U^\dagger U = I) を満たします。QTMのテープはqubit列で、重ね合わせ状態を扱い、ヘッド移動が量子的に並列化されます。
2. 量子回路による実装 (PennyLane例)
QFTはHadamard (H) ゲートと制御位相 (CPhase) ゲートで構築。PennyLaneのようなライブラリでシミュレート可能です。以下は4 qubitのコード例:import pennylane as qml
import numpy as np
dev = qml.device('default.qubit', wires=4)
def qft(wires):
n = len(wires)
for j in range(n):
qml.Hadamard(wires=wires[j])
for k in range(j + 1, n):
qml.CPhase(2 * np.pi / (2 ** (k - j)), wires=[wires[j], wires[k]])
# 出力順序反転のためのSWAP
for j in range(n // 2):
qml.SWAP(wires=[wires[j], wires[n - 1 - j]])
@qml.qnode(dev)
def qft_circuit():
# 例: |0010> を準備
qml.PauliX(wires=1)
qft(range(4))
return [qml.expval(qml.PauliZ(w)) for w in range(4)]
print(qft_circuit())
この回路はHゲートで重ね合わせを作成し、CPhaseで位相回転を適用。SWAPでMSB/LSBを反転します。実行結果はQFT後の期待値ベクトル。回路図は上記の画像を参照。
3. QTMでの実装詳細
QTMでは、QFTをユニタリ演算子として実装。遷移関数δ: (状態q, 読み込みシンボルs) → ∑ α_{q', s', d} |q', s', d⟩ (αは振幅、ユニタリ)。具体的に:
- テープ準備: 入力jをバイナリでテープに書き、qubitとして扱う。補助テープで計算。
- Hadamardシミュレーション: QTMの遷移でHゲートを適用。各qubitに1/√2 (|0⟩ + |1⟩) を生成。ヘッドがqubit位置を重ね合わせて移動。
- CPhaseシミュレーション: 制御qubitの状態に基づき、対象qubitに位相 e^{2πi / 2^k} を加算。QTMの多テープ版で並列処理。
- 時間複雑度: QTMでO(n^2)ステップ。古典シミュレーション(例: FTSimulator in C++)では密度行列ρをQFT ρ QFT^\daggerで計算、12 qubitまで可能だが指数時間。
- NMR実装例: 3 qubit NMR量子コンピュータでQFTを実装。状態トモグラフィーで忠実度を測定、QTMの物理的アナログとして機能。
業界話: 2025年現在、QFTはIBM QiskitやGoogle Cirqで実装され、量子優位性のベンチマーク。QTMは理論的で、実際の量子機は回路モデルですが、等価性によりQTMで証明可能です。詳細なシミュレーションが必要なら、さらに掘り下げます!
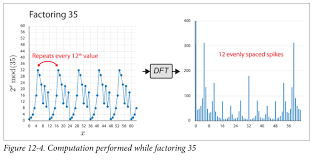
Quantum Fourier Transform (QFT) の Shor's algorithm への応用について詳しく解説します。Shor's algorithm は量子コンピュータで大整数を効率的に素因数分解するアルゴリズムで、1994年に Peter Shor によって提案されました。QFT はこのアルゴリズムの核心部分で、周期関数から周期を抽出する役割を果たします。これにより、古典コンピュータでは指数時間かかる問題を多項式時間で解けます。雑学として、QFT は古典的な離散フーリエ変換 (DFT) の量子版で、量子並列性を活かして指数的に高速化されています。
Shor's Algorithm の概要
Shor's algorithm は、N (分解対象の整数) の素因数分解を、y^x mod N (y はランダム選択) の周期 r を求める問題に帰着させます。r が偶数なら、gcd(y^{r/2} ± 1, N) で因子を得られます。量子部分は周期検出で、QFT が鍵です。
QFT の役割
QFT は量子位相推定 (QPE) の一部として機能し、周期関数 f(x) = y^x mod N の周期 r を抽出します。量子状態の重ね合わせで多くの x を並列評価し、QFT で振幅の干渉を起こして周期の逆数 (1/r) にピークを生じさせます。これにより、測定で r の近似値を得ます。
詳細なステップ
- 初期化: 2つの量子レジスタを準備。第一レジスタ (t qubit, t ≈ 2 log N) を均一重ね合わせに (Hadamard ゲート)。第二レジスタを |1⟩。
- 関数評価: 第一レジスタの値 x で第二レジスタに y^x mod N を計算 (量子並列)。状態: (1/√Q) ∑_x |x⟩ |y^x mod N⟩ (Q=2^t)。
- 第二レジスタの測定: 測定で z = y^k mod N を得、第一レジスタが周期的重ね合わせに崩壊: ∑_m |k + m r⟩ (m=0..)。
- QFT の適用: 第一レジスタに QFT を適用。周期的状態を周波数ドメインに変換し、ピーク at l ≈ (Q / r) * j (j=0,1,..r-1) 。
- 測定とポスト処理: 第一レジスタを測定し、l/Q の連分数展開で r を推定。失敗時は繰り返し。
QFT がなければ、周期検出が古典的に O(√N) 試行必要ですが、QFT で O(log N) 時間に短縮されます。
数学的背景
QFT: |x⟩ → (1/√Q) ∑_k exp(2π i x k / Q) |k⟩。周期状態 ∑_m exp(2π i (k + m r) ω) で干渉し、ω = 2π / Q でピークを生む。例: N=35 の分解で、周期12の信号がQFT後12の等間隔ピークに。
2025年現在、Shor's はポスト量子暗号の動機付けで、QFT の実装が量子機のベンチマークです。詳細なシミュレーションが必要なら、教えてください!




0 件のコメント:
コメントを投稿