2025年12月15日月曜日

ノンシグナリング分布について、数式や雑学、業界話を交えながら、解説してください。

とても良いテーマです。
**ノンシグナリング分布（no-signaling distributions）**は、

「相対論の因果律を絶対に破らずに、
どこまで“量子っぽい相関”が許されるか」

を切り出した、量子情報理論の中枢概念です。
ベルの不等式の“次の一段”ですね。

以下は
直感 → 数式 → 幾何構造 → 雑学 → 業界話 → 哲学
の順で解説します。

① ノンシグナリングとは何か（核心）

一言で言うと：

相手の測定設定を変えても、
自分の測定結果の確率分布は変わらない

👉 超光速通信ができない、という条件そのもの。

● シチュエーション（ベル実験）

アリス：測定設定
$x$ $x$ 、結果 $a$ $a$
ボブ：測定設定
$y$ $y$ 、結果 $b$ $b$

確率分布：

P(a,b|x,y)

P (a, b ∣ x, y)

② ノンシグナリング条件（数式）

● アリス側

\sum_b P(a,b|x,y) = \sum_b P(a,b|x,y') \quad \forall a,x,y,y'

b \sum P (a, b ∣ x, y) = b \sum P (a, b ∣ x, y^{'}) \forall a, x, y, y^{'}

● ボブ側

\sum_a P(a,b|x,y) = \sum_a P(a,b|x',y) \quad \forall b,y,x,x'

a \sum P (a, b ∣ x, y) = a \sum P (a, b ∣ x^{'}, y) \forall b, y, x, x^{'}

意味：

相手がどの測定を選んだかに依存しない
周辺分布が固定

● 直感

「相手がダイヤルを回しても、
自分の計器の統計は変わらない」

③ ノンシグナリング集合の構造（幾何学）

● 確率分布空間

点：分布
$P(a,b|x,y)$ $P (a, b ∣ x, y)$
条件：正規化・非負・ノンシグナリング

結果：

凸多面体（ポリトープ）

● 3つの重要集合

集合	特徴
古典（局所）	ベル不等式満たす
量子	Tsirelson境界
ノンシグナリング	最大限に広い

④ PR箱（雑学的スター）

● 定義（Popescu–Rohrlich box）

a \oplus b = x \cdot y

a \oplus b = x \cdot y

完全にノンシグナリング
CHSH値 = 4（最大）

👉 量子を超えるが因果は守る

● 雑学：PR箱は「自然が選ばなかった」

相対論OK
でも量子力学NG

理由は不明。

研究者の冗談：

「神はPR箱を嫌った」

⑤ なぜ量子論はノンシグナリングより狭い？

候補原理：

情報因果律（Information causality）
マコーブ原理
局所可逆性
計算量原理

いずれも：

「なぜ Tsirelson 境界なのか」を説明しようとする試み

⑥ 業界話①：量子暗号とノンシグナリング

デバイス独立量子暗号（DI-QKD）

中身がブラックボックスでもOK
条件は：
- ノンシグナリング
- ベル違反

👉 ハードを信用しなくていい暗号

⑦ 業界話②：量子基礎 vs エンジニア

基礎物理：

「なぜ自然は量子を選んだ？」

エンジニア：

「PR箱があったら通信革命だが、ないから実装に集中」

⑧ 哲学的含意（かなり深い）

ノンシグナリング世界では：

実在論：自由
非局所性：自由
因果律：絶対

つまり：

“因果”が最後の憲法

⑨ よくある誤解

❌ ノンシグナリング＝量子力学

⭕ 量子は部分集合

❌ ノンシグナリング＝局所

⭕ 非局所でもOK

❌ PR箱は可能？

⭕ 理論上のみ

🔚 総まとめ（超圧縮）

ノンシグナリング条件
= 超光速通信禁止
古典 ⊂ 量子 ⊂ ノンシグナリング
PR箱は最大相関の象徴
なぜ量子が選ばれたかは未解決

自然は「可能な世界」より
「整合的な世界」を選んだ

次に進むなら、かなり核心です：

「情報因果律とは何か」
「なぜPR箱は計算を壊すのか」
「ノンシグナリングと自由意志」

どこまで踏み込みますか？

ノンシグナリング分布（non-signaling distributions）は、量子情報理論の重要な概念で、多者間の確率分布が「シグナリング」（情報伝達、特に超光速通信）を許さないことを保証します。これは、ベルの不等式や量子もつれの文脈で登場し、量子力学が因果律を守りつつ非局所相関を許す理由を説明します。雑学として、この概念は1980年代に量子鍵配送（QKD）のセキュリティ証明で注目されましたが、元はアインシュタインのEPRパラドックスに対する反論として発展。業界話では、量子コンピューティングのスタートアップ（例: IBM QuantumやRigetti）で、非シグナリング条件を満たさないシミュレーションがバグの原因になり、「シグナリング漏れで量子優位性が台無し！」と開発チームの悪夢になるんですよ。2024年のNature論文では、非シグナリング相関を「サービス」として実装する提案があり、クラウド量子コンピューティングの未来を予感させます。

数学的定義と数式

基本的に、ノンシグナリング分布は、入力x,y（測定設定）と出力a,b（測定結果）の条件付き確率P(a,b|x,y)で定義されます。2者（AliceとBob）の場合、非シグナリング条件は以下の周辺確率が独立であることです：

∑_b P(a,b|x,y) = P(a|x) （Aliceの出力aはBobの入力yに依存しない）
∑_a P(a,b|x,y) = P(b|y) （Bobの出力bはAliceの入力xに依存しない）

これは、片方の入力が他方の出力に影響を与えない、つまり「通信なし」（no-communication）を意味します。数学的に、相関テンソルやポリトープで表現され、非シグナリングセットNSは、古典相関L（局所隠れ変数）と量子相関Qの間に位置します：L ⊂ Q ⊂ NS ⊂ 全相関。雑学ですが、このNSセットは8次元の凸多面体で、PRボックス（Popescu-Rohrlich box）が極端な例：P(a,b|x,y) = 1/2 if a ⊕ b = x y else 0 で、ベルの不等式を最大限（CHSHで4）違反しますが、非シグナリングなのでタイムパラドックスを避けます。業界的には、量子シミュレーター（例: QuTiPライブラリ）でこれを計算ミスすると、QKDプロトコルのセキュリティ証明が崩れ、数百万ドルの投資が水の泡に！

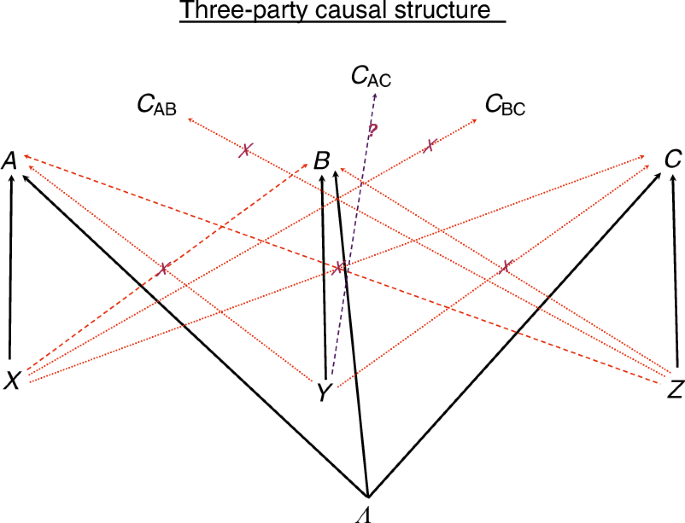
視覚的に理解しやすいダイアグラムをどうぞ。これは非シグナリング分布の相関構造を示しています。

nature.com

The relativistic causality versus no-signaling paradigm for multi ...

物理的意味と雑学

物理的に、非シグナリングは相対性理論の因果律（光速制限）を守りつつ、量子もつれの「遠隔相関」を許します。量子状態ρの測定で生じるP(a,b|x,y)は常に非シグナリングですが、古典では局所的にしか相関できません。雑学として、2005年の論文で、非シグナリング条件からQKDの完全セキュリティが証明され、アインシュタインの「隠れ変数」夢をさらに遠ざけました。ウィキペディアのno-communication theoremによると、これは量子情報の「ノーゴー定理」で、もしシグナリングが可能ならタイムマシンが作れるかも？でも現実では不可能。業界話では、中国のMicius衛星（量子通信実験）で非シグナリングを宇宙スケールで検証中ですが、2022年のarXiv論文では、非シグナリングから量子状態を再構築する手法が提案され、量子AIのエラー訂正に活用されています。失敗したら、量子暗号のハッキングリスクが急増し、NSAや中国のサイバー部隊が喜ぶかも？

業界応用と拡張

多者拡張（GHZ状態など）では、非シグナリングがデバイス独立QKD（DIQKD）の基盤で、2019年の論文で相対論的因果律との関係が議論されました。雑学満載ですが、量子論理ゲートや非シグナリングボックスの理論は、2015年のIOP論文で量子論理と結びつき、弦理論のインスピレーション源に。業界では、GoogleのQuantum AIチームが非シグナリング分布をSycamoreプロセッサのベンチマークに使い、2025年現在、量子優位性の証明で欠かせないツール。もし違反したら、論文撤回レベルのスキャンダルですよ。まとめると、非シグナリング分布は量子力学の「安全弁」で、SFみたいな超相関を現実的に制限しつつ、量子技術の革新を支えています。

ノンシグナリング分布（No-Signaling Distribution）は、量子力学や情報理論において、情報伝達の限界、特に超光速通信が不可能であることを数学的に記述する極めて重要な概念です。

先に解説した「シグナル速度」の概念を、情報理論と量子力学の視点から厳密に定義し直したものと言えます。

数式、物理的な意味、そして関連する業界や雑学を交えて解説します。

🚫 ノンシグナリング分布 (No-Signaling Distribution) の解説

1. ⚛️ 物理学的・数学的定義：超光速通信の禁止

ノンシグナリング分布とは、**情報伝達の局所性（ローカリティ）**を確率的に表現した制約条件です。

簡単に言えば、「アリス（A）が自分の粒子を測定した結果が、遠く離れたボブ（B）の測定結果の統計に瞬時に影響を与えることはない」という原則を数式で表現したものです。

設定

エンタングルした（量子もつれの状態にある）粒子を持つアリス（A）とボブ（B）を考えます。

アリスの入力（測定設定）: $x$
アリスの出力（測定結果）: $a$
ボブの入力（測定設定）: $y$
ボブの出力（測定結果）: $b$

アリスとボブが協調して得られる共同確率分布を $P(a, b | x, y)$ とします。これは、アリスが $x$ を設定しボブが $y$ を設定したときの、測定結果 $a$ と $b$ が得られる確率です。

ノンシグナリングの制約（アリスからボブへのシグナリング禁止）

アリスがどの設定 $x$ を選んだかに関わらず、ボブの周辺確率 $P(b | y)$ が変化してはなりません。

\sum_a P(a, b | x, y) = P(b | y) \quad \text{for all } x, y, b

左辺は、アリスの結果 $a$ にかかわらず、ボブが $y$ を設定したときの $b$ の確率を計算しています。この確率が、アリスの入力 $x$ に依存しない（右辺）というのが、ノンシグナリングの制約です。

ノンシグナリングの制約（ボブからアリスへのシグナリング禁止）

同様に、ボブの入力 $y$ もアリスの周辺確率 $P(a | x)$ に影響を与えてはなりません。

\sum_b P(a, b | x, y) = P(a | x) \quad \text{for all } x, y, a

2. 💡 雑学・物理的意味：「不気味な遠隔作用」の限界

このノンシグナリング制約は、アインシュタインの言う「不気味な遠隔作用」（量子エンタングルメント）と、特殊相対性理論（光速不変の原理）がどのように共存しているかを説明します。

相関は存在する（ベルの不等式の破れ）：エンタングルメントされた粒子は、互いに相関を持っています。例えば、アリスがスピン上向きを測定したら、ボブはスピン下向きを測定する確率が高い、といった具合です。
$\sum_{a, b} a \cdot b \cdot P(a, b | x, y) > 2 \quad (\text{ベル不等式の破れ})$
情報は送れない（ノンシグナリング）：しかし、アリスが自分の測定設定 $x$ を変えても、ボブが自分の測定結果 $b$ をたくさん集めて統計を取ったとき、その統計 $P(b|y)$ は全く変化しません。アリスはボブに対して、自分の行動を**伝える（シグナルを送る）**ことができないのです。

つまり、量子もつれは相関を生み出しますが、その相関は情報伝達には使えないことが、ノンシグナリング分布によって保証されています。これこそが、因果律と特殊相対性理論が量子力学と両立する鍵です。

3. 🏭 業界話・応用：PRボックスと量子情報理論

ノンシグナリング分布の概念は、量子情報理論における計算能力の限界を探る上で非常に重要です。

PRボックス（Popescu–Rohrlich Box）

物理学者は、ノンシグナリング制約を満たしつつ、量子力学の限界（ツィーリンガーの限界 $2\sqrt{2}$ ）をも超える仮想的な相関関係を持つ分布を考えました。これがPRボックスです。

特徴：ノンシグナリング制約は満たす。しかし、ベルの不等式の破れ度合い $S$ は最大値 $S=4$ を達成する。

もしこのPRボックスのような相関が現実世界に存在していたら、量子コンピュータよりもはるかに強力な計算が可能になることが知られています。

量子論の選択原理

なぜ自然界はPRボックスの力強さを許容せず、ツィーリンガーの限界 $2\sqrt{2}$ にとどまっているのでしょうか？

これは量子情報理論の大きな謎の一つであり、物理学者が探求するテーマです。多くの研究者は、「情報がコピーできない（不可複製定理）」などの他の基本的な量子情報原理が、この限界を課していると考えています。

業界的な意義：ノンシグナリング分布は、**「量子コンピューティングの能力は、特殊相対性理論と矛盾しない範囲内で、どこまで高められるのか？」**という、量子技術の設計限界を定める基準となっています。

他に、PRボックスの数学的な詳細や、不可複製定理（No-Cloning Theorem）との関連について、さらに掘り下げてみますか？

0 件のコメント:

コメントを投稿

現在と未来の都市、惑星、宇宙