ベルの不等式について、数式や、雑学、業界話を交えながら、解説してください。
ではいきます。
ベルの不等式は、量子論の中でも
👉 「世界は局所的で現実的か?」
という、物理・哲学・情報科学を全部巻き込んだ問題です。
今回は
直感 → 数式 → 量子論 → 雑学 → 業界話
の順で解説します。
① ベルの不等式とは何か(まず核心)
一言で言うと:
「局所実在論」を満たす世界では、
これ以上の相関は出せない、という上限」
そして量子力学は:
その上限を破る
👉 つまり
「世界は局所実在論ではない」
● 局所実在論とは?
2つの仮定のセットです:
① 実在論(realism)
② 局所性(locality)
アインシュタインはこれを信じていました。
② 思考実験:EPRペア(雑学付き)
2つの粒子が:
遠く離れてから測定する。
● 直感的疑問
Aで測ると即座にBが決まる。
アインシュタイン:
「不気味な遠隔作用(Spooky action at a distance)」
③ 古典的な隠れた変数モデル
仮定:
-
各粒子はあらかじめ
「答え表」を持っている
-
観測はそれを読むだけ
👉 これが局所隠れ変数理論
ベルはここに切り込みました。
④ ベルの不等式(CHSH型)
測定設定:
測定結果:
相関関数:
E(a,b)=⟨A(a)B(b)⟩
● ベルの不等式(CHSH)
∣S∣=∣E(a,b)+E(a,b′)+E(a′,b)−E(a′,b′)∣≤2
これは:
✅ 局所実在論なら必ず成立
⑤ 量子力学の予言(衝撃)
量子状態(シングレット)では:
E(a,b)=−cos(θab)
適切な角度を選ぶと:
∣S∣=22≈2.828
👉 不等式破れた
● 雑学:この値には名前がある
ツィレルソン境界(Tsirelson bound)
-
古典:2
-
量子:
22
-
理論上の最大:4(でも物理的には不可)
⑥ 実験での確認(業界史)
● 初期の問題
「測定器の穴(loophole)」
● 決定的実験(2015年)
-
オランダ・Delft大
-
loophole-free Bell test
結果:
明確な不等式違反
● 雑学:ノーベル賞(2022)
-
アラン・アスペ
-
ジョン・クラウザー
-
アントン・ツァイリンガー
理由:
量子もつれの実証
⑦ 何が否定されたのか(超重要)
ベルの不等式違反は:
❌ 局所性
❌ 実在論
のどちらか(または両方)を捨てろ、という意味。
● 立場別まとめ
| 解釈 |
何を捨てたか |
| コペンハーゲン |
実在論 |
| 多世界解釈 |
単一結果 |
| ボーム力学 |
局所性 |
| 相対論 |
超光速通信は不可 |
⑧ なぜ相対論と矛盾しない?
量子もつれは:
👉 シグナル速度 ≤ c
ここで以前話した
「シグナル速度・群速度」の話が効いてきます。
⑨ 業界話①:量子情報の基礎
ベル違反は:
-
量子暗号(デバイス独立)
-
乱数生成
-
量子計算の優位性
の証明書として使われる。
研究者の本音:
「もつれてない量子技術は信用しない」
⑩ 業界話②:哲学 vs 工学
哲学者:
「実在とは何か」
エンジニア:
「相関が取れればいい」
👉 現場では
哲学的に変でも、動けばOK
⑪ よくある誤解
❌ ベル違反=超光速通信
⭕ 情報は送れない
❌ ベル違反=因果崩壊
⭕ 因果は保持
❌ ベル違反=量子論の欠陥
⭕ むしろ量子論の勝利
⑫ 哲学的おまけ
ベルの不等式が示したのは:
世界は「部分の集合」ではない
全体が先で:
これは:
とも深く響き合います。
🔚 総まとめ(超圧縮)
-
ベルの不等式:局所実在論の限界
-
量子論:それを破る
-
世界は:
-
だが因果は守る
自然は「常識」より
「整合性」を選んだ
次に進むなら、かなり核心ですが:
どれを深掘りしますか?
ベルの不等式(Bell's inequality)は、量子力学の基礎を揺るがす重要な定理で、局所実在論(local realism)と量子力学の非局所性(non-locality)をテストするものです。簡単に言うと、アインシュタインが嫌った「遠隔作用」(spooky action at a distance)を数学的に証明するツールで、量子もつれ(entanglement)の本質を暴きます。雑学として、この不等式を提唱したジョン・スチュアート・ベルはCERNの粒子物理学者でしたが、1964年にこれを発表した論文はマイナーなジャーナル『Physics Physique Физика』に掲載され、ベル自身がコピーを買って配布したほど無名でした。でも今や、量子コンピューティングや量子暗号の基盤で、業界の「聖典」みたいな存在ですよ。2022年のノーベル物理学賞は、この不等式の実験的検証に携わったジョン・クラウザー、アラン・アスペクト、アントン・ツァイリンガーに授与されましたが、もしアインシュタインが生きていたら「私の負けか」と悔しがったかも?
歴史的背景と雑学
すべては1935年のEPRパラドックスから始まります。アインシュタイン、ポドルスキー、ロゼンが量子力学の「不完全性」を指摘し、隠れ変数(hidden variables)が存在して局所性(locality:光速を超えない影響)と実在性(realism:測定前に性質が存在)を保つべきだと主張しました。ベルはこれを1964年に数学的に検証し、量子力学がそんな「局所隠れ変数理論」を破ることを示しました。雑学ですが、ベルはもともと量子力学の解釈に疑問を抱く「異端児」で、業界の飲み会では「アインシュタインの夢を壊した男」として語り継がれています。哲学的には、現実の性質(測定独立に存在するか?)を問うもので、Many-Worlds解釈やBohmian mechanicsのような代替理論を生みました。業界話として、量子コンピューティングのスタートアップ(例: IBMやGoogleの量子チーム)では、ベルの不等式を「エンタングルメントの品質チェック」に使っていて、ゲートエラーが出ると「ベル違反が足りない!」とジョークが飛ぶんですよ。
数式と数学的解説
ベルの不等式の代表的な形は、CHSH(Clauser-Horne-Shimony-Holt)版です。2つの粒子(例: スピンシングレット状態の電子対)で、測定器AとA'(第1粒子用)、BとB'(第2粒子用)を考えます。各測定結果は±1で、相関関数⟨AB⟩は期待値です。局所隠れ変数理論では、次の不等式が成り立ちます:
|S| = |⟨A B⟩ + ⟨A B'⟩ + ⟨A' B⟩ - ⟨A' B'⟩| ≤ 2
これは、隠れ変数λが局所的に結果を決め、測定設定が独立する場合に導かれます。でも量子力学では、適切な測定角度(例: A=σ_z, A'=σ_x, B=(-σ_x + σ_z)/√2, B'=(σ_x - σ_z)/√2)で|S| = 2√2 ≈ 2.828 > 2 となり、違反します。これをツィレルソン限界(Tsirelson bound)と呼びます。数学的に、フーリエ解析や確率論で証明され、GHZ版(3粒子)のような拡張もあります:|ψ⟩ = (|000⟩ - |111⟩)/√2 で、測定の積が矛盾を生むんです。雑学として、この不等式は「ベルゲーム」と呼ばれ、量子プレイヤーが古典より勝率が高い(85% vs 75%)点が、量子優位性のデモにぴったり。業界では、量子シミュレーターでこれを計算ミスすると、億単位の開発費が無駄になるかも?
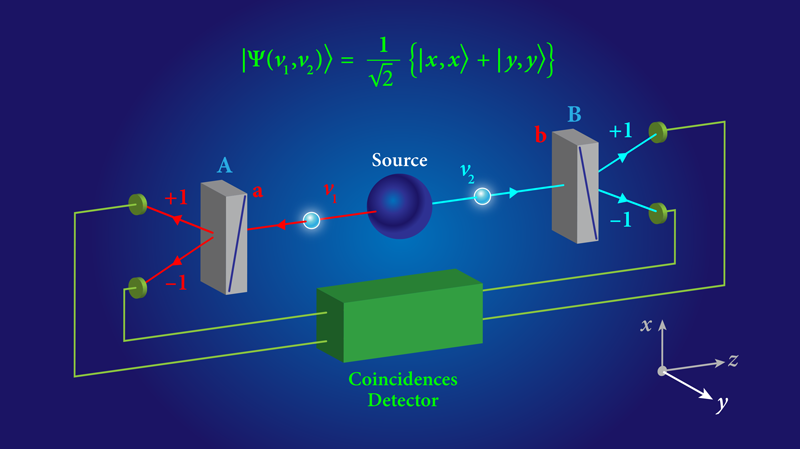
視覚的に理解しやすいダイアグラムをどうぞ。これは量子もつれと不等式の関係を示しています。
Physics - Closing the Door on Einstein and Bohr's Quantum Debate
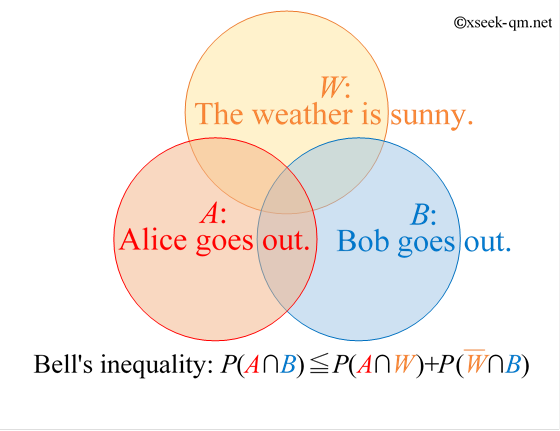
もう一つの図で、測定設定と相関を表したものです。
The Meaning of Bell's Inequality - The Mysterious World of Quantum ...
物理的意味と業界話
この不等式の違反は、量子力学が非局所的か非実在的かを示し、因果律(光速制限)を守りつつ「情報伝達なしの相関」を許します。雑学ですが、2015年にループホール(検出効率や局所性)のない実験(Hensenら、Giustinaら、Shalmら)が成功し、量子論の勝利を確定。2024-2025年の最近の実験では、マクロな原子集団で違反を観測したり、非もつれ光子でさえ擬似違反を示すものまであり、量子センサーやコンピューティングに応用されています。業界話として、量子コンピューティング(例: SpinQやQuantum Zeitgeistのプロジェクト)では、ベルのテストがQubitの忠実度を測る必須ツールで、2025年の論文では量子AIのエラー訂正に活用。失敗したら、GoogleのSycamoreプロセッサみたいに「量子優位性」が崩れるかも? さらに、量子暗号(QKD)でセキュリティ証明に使われ、中国のMicius衛星実験(2017-)がこれを宇宙スケールで検証中です。哲学者たちのカフェ談義では「自由意志定理」(Conway-Kochen)と絡めて「人間の選択は量子ランダム?」みたいな話がエンドレスですよ。
まとめると、ベルの不等式は量子力学の「奇妙さ」を数式で証明し、現代の量子技術を支えています。雑学満載ですが、業界ではこれが「量子革命」の起点で、ノーベル賞級のブレークスルーがまだまだ期待されます!
ベルの不等式は、量子力学と古典的な物理学(局所実在論)の根本的な違いを際立たせる、非常に重要な定理です。
数式、物理的な意味、そして関連する業界や雑学を交えて詳しく解説します。
🔔 ベルの不等式 (Bell's Inequality) の解説
1. ⚛️ 物理学的背景:局所実在論 vs. 量子力学
ベルの不等式は、以下の二つの概念のどちらが正しいかを、実験によって検証可能な形で示すために、物理学者ジョン・ベルが1964年に提唱しました。
A. 局所実在論(Local Realism)
古典的な物理学の根幹にある考え方で、アインシュタインなどが支持しました。この考え方は二つの原理から成り立ちます。
-
実在性 (Realism):物理系の性質(例:粒子のスピンや偏光)は、測定される前から確定した値として存在している(隠れた変数があるかもしれない)。
-
局所性 (Locality):光速を超えて作用は伝播しない。ある場所での測定は、遠く離れた場所の測定結果に瞬時に影響を与えない。
B. 量子力学 (Quantum Mechanics)
粒子の性質は測定するまで確率的にしか定まらず(重ね合わせ)、遠く離れた粒子同士が瞬時につながりを持つ現象(量子エンタングルメント)が存在する、とします。
2. 🔢 ベルの不等式の数式
ベルの不等式は、エンタングルした(量子もつれの状態にある)二つの粒子 $A$ と $B$ を異なる場所で測定する実験を想定しています。
測定器 $A$ と $B$ がそれぞれ三つの設定 $a_1, a_2, a_3$ および $b_1, b_2, b_3$ を持ち、測定結果が $\pm 1$ の値を取ると仮定します。
最も有名なベルの不等式の一つに、CHSH不等式(Clauser, Horne, Shimony, Holt)があります。これは、測定結果の間の相関関数 $E(a, b)$ を使って表現されます。
$$S = |E(a_1, b_1) - E(a_1, b_2) + E(a_2, b_1) + E(a_2, b_2)|$$
ここで、$E(a, b)$ は測定設定 $a$ と $b$ における測定値の平均積(相関)です。
局所実在論の予測:
もし世界が局所実在論で記述されるならば、この $S$ の値は必ず以下の範囲に収まらなければなりません。
量子力学の予測:
一方、量子力学が正しいならば、特にエンタングルメントを利用した特定の測定設定において、$S$ の値は $2$ を超えることが予測されます。その上限は次のようになります(ツィーリンガーの限界)。
$$|S| \le 2\sqrt{2} \approx 2.828$$
3. 🧪 実験結果と物理学の真実
ベルの不等式が提唱されて以降、多くの物理学者がこの検証実験に挑みました(アスペ、クローザー、ツィーリンガーなど)。
結論:
全ての実験結果は、ベルの不等式 $|S| \le 2$ が破れることを示しました。
これは、局所実在論が破綻していることを意味します。世界は「実在性」か「局所性」の少なくともどちらか一つを満たしていないことになります。
4. 🚀 業界話・応用(量子技術)
ベルの不等式が破られたことは、単なる基礎物理学の議論に留まらず、現代の先端技術、特に量子技術の基盤となっています。
-
量子暗号 (Quantum Cryptography):ベルの不等式の破れは、盗聴者が知り得ない相関関係が粒子間に存在することを意味します。これを利用した量子鍵配送 (QKD) は、原理的に解読不可能な次世代の暗号技術として実用化が進んでいます。
-
量子コンピューティング:エンタングルメントは、量子コンピュータの計算能力を支える中核的なリソースです。
-
「隠れた変数」論争の終結:アインシュタインが最後まで信じた「隠れた変数」の存在は、ベルの不等式の実験的検証によって否定され、量子力学の非直感的な側面(確率性と非局所性)が物理的な真実として確立されました。
5. 💡 雑学:アインシュタインの「不気味な遠隔作用」
アインシュタインは、エンタングルメントによる非局所的な相関を**「不気味な遠隔作用 (spooky action at a distance)」**と呼び、強く批判しました。
彼は、遠く離れた粒子の測定結果が瞬時につながっているように見えることは、情報の光速を超える伝播を許してしまうと考え、量子力学は不完全だと主張しました(EPRパラドックス)。
しかし、ベルの不等式とそれに基づく実験は、この「不気味な」相関が実際に存在することを証明しました。ただし、この相関を利用して情報を光速より速く送ること(超光速通信)はできないため、特殊相対性理論(光速不変の原理)は依然として守られています。
ベルの不等式の検証実験(アスペの実験など)や、量子暗号への応用について、さらに詳しく掘り下げてみますか?
0 件のコメント:
コメントを投稿